AUTOKD: Automatic Knowledge Distillation Into A Student Architecture Family

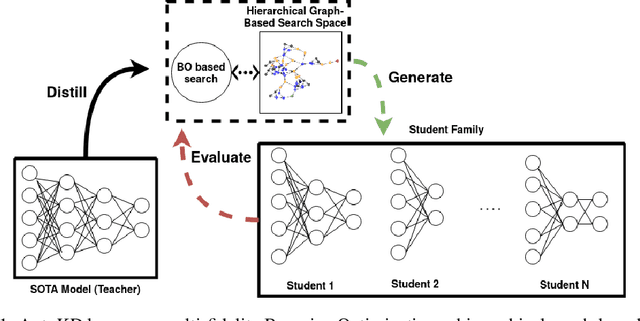
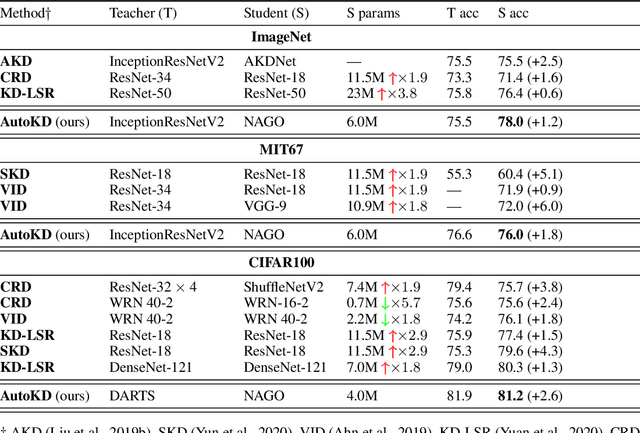
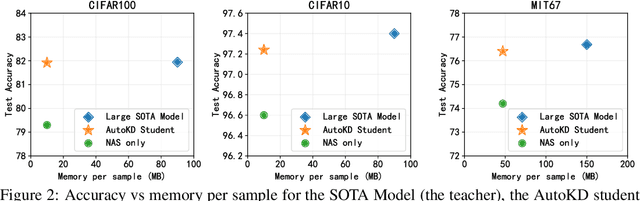
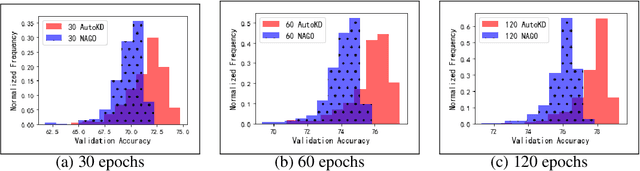
State-of-the-art results in deep learning have been improving steadily, in good part due to the use of larger models. However, widespread use is constrained by device hardware limitations, resulting in a substantial performance gap between state-of-the-art models and those that can be effectively deployed on small devices. While Knowledge Distillation (KD) theoretically enables small student models to emulate larger teacher models, in practice selecting a good student architecture requires considerable human expertise. Neural Architecture Search (NAS) appears as a natural solution to this problem but most approaches can be inefficient, as most of the computation is spent comparing architectures sampled from the same distribution, with negligible differences in performance. In this paper, we propose to instead search for a family of student architectures sharing the property of being good at learning from a given teacher. Our approach AutoKD, powered by Bayesian Optimization, explores a flexible graph-based search space, enabling us to automatically learn the optimal student architecture distribution and KD parameters, while being 20x more sample efficient compared to existing state-of-the-art. We evaluate our method on 3 datasets; on large images specifically, we reach the teacher performance while using 3x less memory and 10x less parameters. Finally, while AutoKD uses the traditional KD loss, it outperforms more advanced KD variants using hand-designed students.

MANAS: Multi-Agent Neural Architecture Search

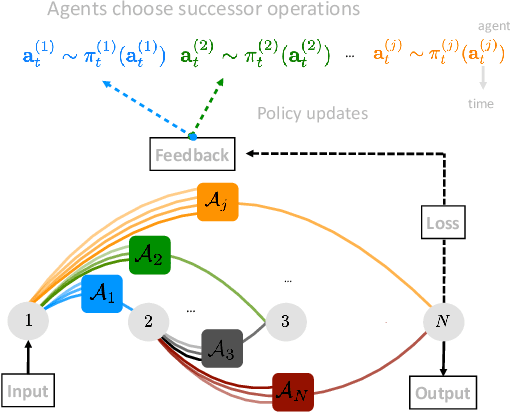
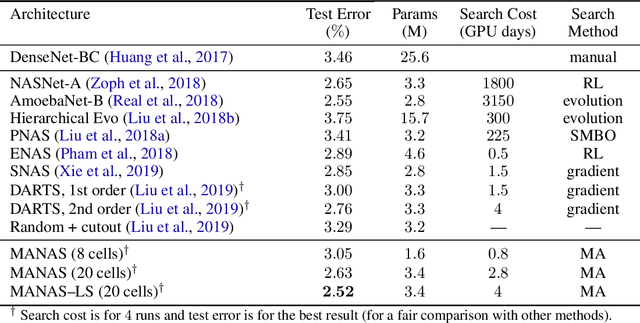
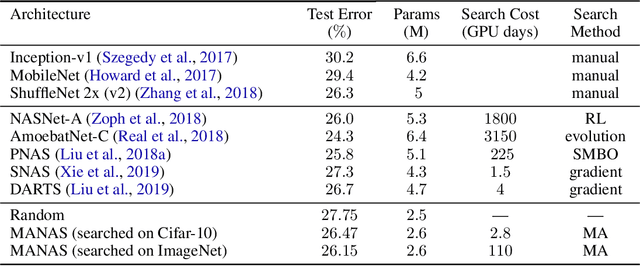
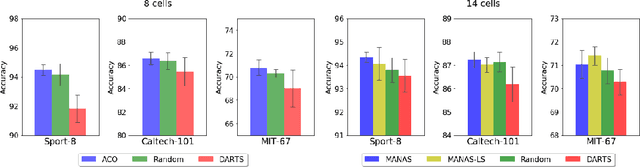
The Neural Architecture Search (NAS) problem is typically formulated as a graph search problem where the goal is to learn the optimal operations over edges in order to maximise a graph-level global objective. Due to the large architecture parameter space, efficiency is a key bottleneck preventing NAS from its practical use. In this paper, we address the issue by framing NAS as a multi-agent problem where agents control a subset of the network and coordinate to reach optimal architectures. We provide two distinct lightweight implementations, with reduced memory requirements (1/8th of state-of-the-art), and performances above those of much more computationally expensive methods. Theoretically, we demonstrate vanishing regrets of the form O(sqrt(T)), with T being the total number of rounds. Finally, aware that random search is an, often ignored, effective baseline we perform additional experiments on 3 alternative datasets and 2 network configurations, and achieve favourable results in comparison.