Modularity Based Community Detection in Hypergraphs

In this paper, we propose a scalable community detection algorithm using hypergraph modularity function, h-Louvain. It is an adaptation of the classical Louvain algorithm in the context of hypergraphs. We observe that a direct application of the Louvain algorithm to optimize the hypergraph modularity function often fails to find meaningful communities. We propose a solution to this issue by adjusting the initial stage of the algorithm via carefully and dynamically tuned linear combination of the graph modularity function of the corresponding two-section graph and the desired hypergraph modularity function. The process is guided by Bayesian optimization of the hyper-parameters of the proposed procedure. Various experiments on synthetic as well as real-world networks are performed showing that this process yields improved results in various regimes.

Predicting Properties of Nodes via Community-Aware Features

A community structure that is often present in complex networks plays an important role not only in their formation but also shapes dynamics of these networks, affecting properties of their nodes. In this paper, we propose a family of community-aware node features and then investigate their properties. We show that they have high predictive power for classification tasks. We also verify that they contain information that cannot be recovered neither by classical node features nor by node embeddings (both classical as well as structural).

Artificial Benchmark for Community Detection with Outliers (ABCD+o)

The Artificial Benchmark for Community Detection graph (ABCD) is a random graph model with community structure and power-law distribution for both degrees and community sizes. The model generates graphs with similar properties as the well-known LFR one, and its main parameter $\xi$ can be tuned to mimic its counterpart in the LFR model, the mixing parameter $\mu$. In this paper, we extend the ABCD model to include potential outliers. We perform some exploratory experiments on both the new ABCD+o model as well as a real-world network to show that outliers possess some desired, distinguishable properties.

Hypergraph Artificial Benchmark for Community Detection (h-ABCD)

The Artificial Benchmark for Community Detection (ABCD) graph is a recently introduced random graph model with community structure and power-law distribution for both degrees and community sizes. The model generates graphs with similar properties as the well-known LFR one, and its main parameter can be tuned to mimic its counterpart in the LFR model, the mixing parameter. In this paper, we introduce hypergraph counterpart of the ABCD model, h-ABCD, which produces random hypergraph with distributions of ground-truth community sizes and degrees following power-law. As in the original ABCD, the new model h-ABCD can produce hypergraphs with various levels of noise. More importantly, the model is flexible and can mimic any desired level of homogeneity of hyperedges that fall into one community. As a result, it can be used as a suitable, synthetic playground for analyzing and tuning hypergraph community detection algorithms.

Properties and Performance of the ABCDe Random Graph Model with Community Structure

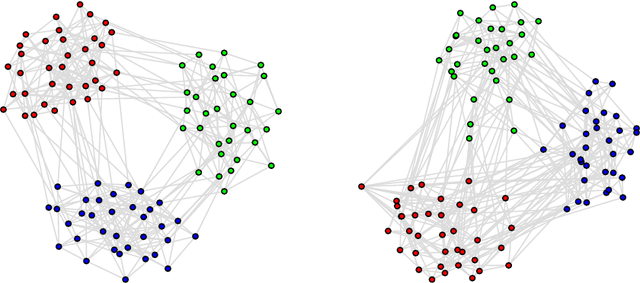
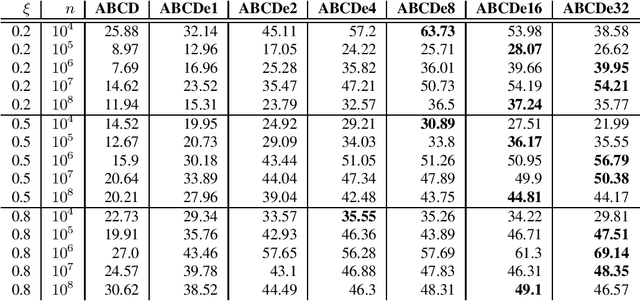
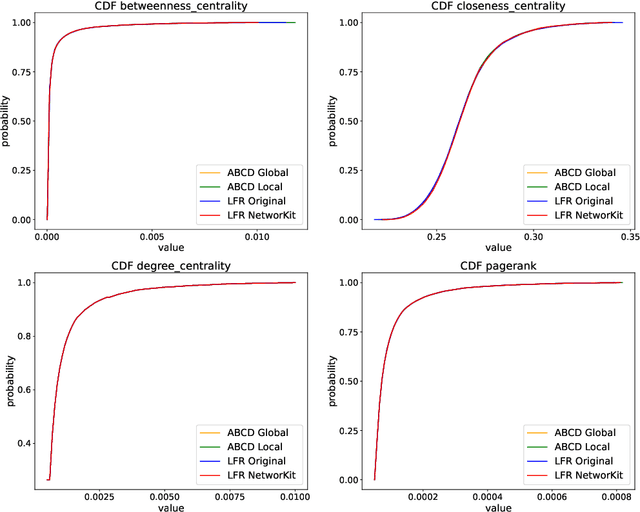
In this paper, we investigate properties and performance of synthetic random graph models with a built-in community structure. Such models are important for evaluating and tuning community detection algorithms that are unsupervised by nature. We propose a new implementation of the ABCD graph generator, ABCDe, that uses multiple-threading. We discuss the implementation details of the algorithm as well as compare it with both the previously available sequential version of the ABCD model and with the parallel implementation of the standard and extensively used LFR generator. We show that ABCDe is more than ten times faster and scales better than the parallel implementation of LFR provided in NetworKit. Moreover, the algorithm is not only faster but random graphs generated by ABCD have similar properties to the ones generated by the original LFR algorithm, while the parallelized NetworKit implementation of LFR produces graphs that have noticeably different characteristics.

Survey of Generative Methods for Social Media Analysis

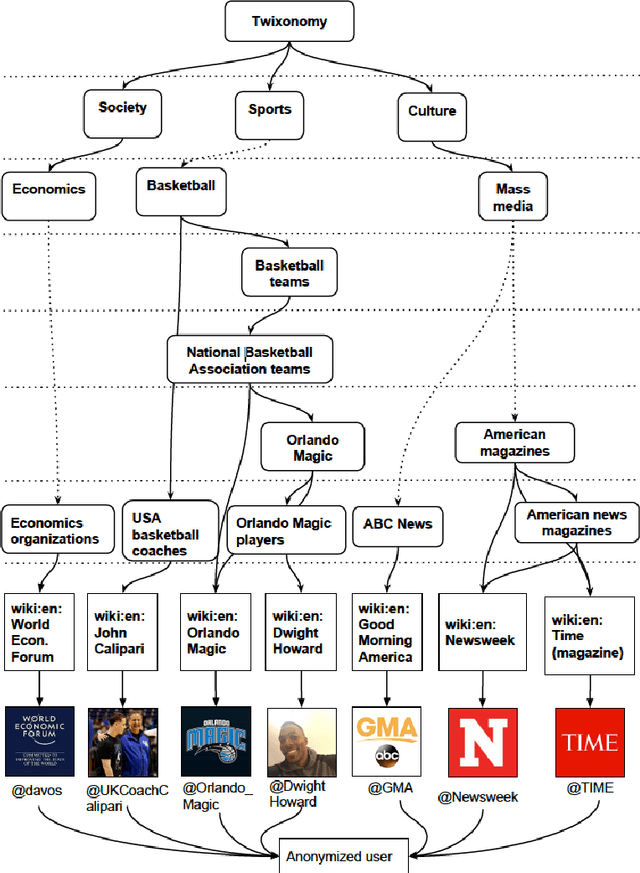
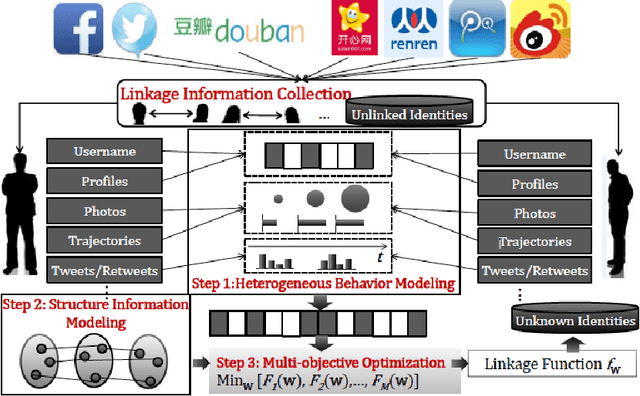
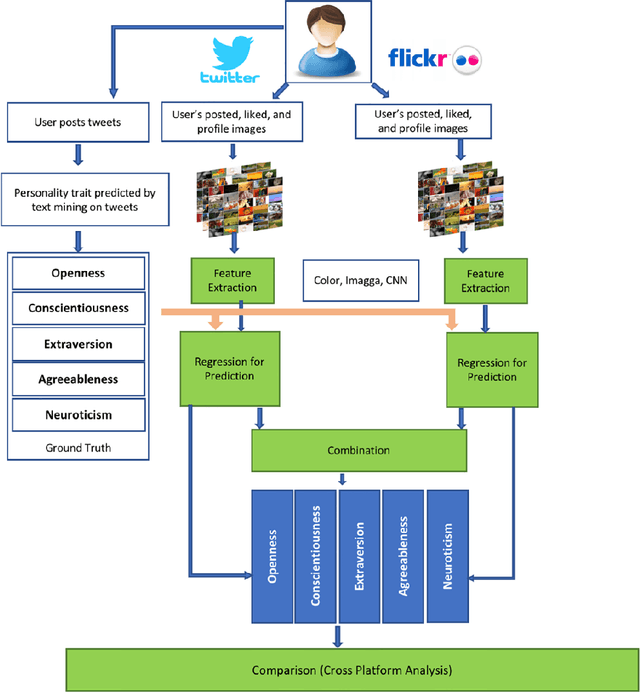
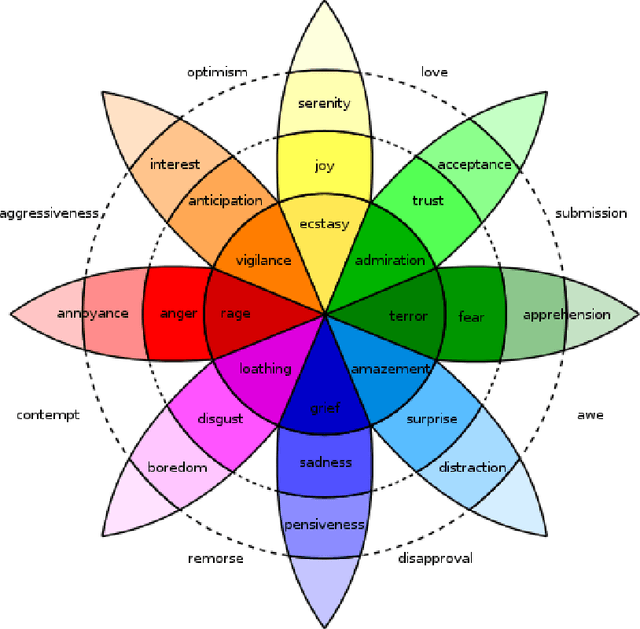
This survey draws a broad-stroke, panoramic picture of the State of the Art (SoTA) of the research in generative methods for the analysis of social media data. It fills a void, as the existing survey articles are either much narrower in their scope or are dated. We included two important aspects that currently gain importance in mining and modeling social media: dynamics and networks. Social dynamics are important for understanding the spreading of influence or diseases, formation of friendships, the productivity of teams, etc. Networks, on the other hand, may capture various complex relationships providing additional insight and identifying important patterns that would otherwise go unnoticed.

A Multi-purposed Unsupervised Framework for Comparing Embeddings of Undirected and Directed Graphs

Graph embedding is a transformation of nodes of a network into a set of vectors. A good embedding should capture the underlying graph topology and structure, node-to-node relationship, and other relevant information about the graph, its subgraphs, and nodes themselves. If these objectives are achieved, an embedding is a meaningful, understandable, and often compressed representation of a network. Unfortunately, selecting the best embedding is a challenging task and very often requires domain experts. In this paper, we extend the framework for evaluating graph embeddings that was recently introduced by the authors. Now, the framework assigns two scores, local and global, to each embedding that measure the quality of an evaluated embedding for tasks that require good representation of local and, respectively, global properties of the network. The best embedding, if needed, can be selected in an unsupervised way, or the framework can identify a few embeddings that are worth further investigation. The framework is flexible, scalable, and can deal with undirected/directed, weighted/unweighted graphs.

Evaluating Node Embeddings of Complex Networks

Graph embedding is a transformation of nodes of a graph into a set of vectors. A~good embedding should capture the graph topology, node-to-node relationship, and other relevant information about the graph, its subgraphs, and nodes. If these objectives are achieved, an embedding is a meaningful, understandable, compressed representations of a network that can be used for other machine learning tools such as node classification, community detection, or link prediction. The main challenge is that one needs to make sure that embeddings describe the properties of the graphs well. As a result, selecting the best embedding is a challenging task and very often requires domain experts. In this paper, we do a series of extensive experiments with selected graph embedding algorithms, both on real-world networks as well as artificially generated ones. Based on those experiments we formulate two general conclusions. First, if one needs to pick one embedding algorithm before running the experiments, then node2vec is the best choice as it performed best in our tests. Having said that, there is no single winner in all tests and, additionally, most embedding algorithms have hyperparameters that should be tuned and are randomized. Therefore, our main recommendation for practitioners is, if possible, to generate several embeddings for a problem at hand and then use a general framework that provides a tool for an unsupervised graph embedding comparison. This framework (introduced recently in the literature and easily available on GitHub repository) assigns the divergence score to embeddings to help distinguish good ones from bad ones.

Artificial Benchmark for Community Detection : Fast Random Graph Model with Community Structure

Most of the current complex networks that are of interest to practitioners possess a certain community structure that plays an important role in understanding the properties of these networks. Moreover, many machine learning algorithms and tools that are developed for complex networks try to take advantage of the existence of communities to improve their performance or speed. As a result, there are many competing algorithms for detecting communities in large networks. Unfortunately, these algorithms are often quite sensitive and so they cannot be fine-tuned for a given, but a constantly changing, real-world network at hand. It is therefore important to test these algorithms for various scenarios that can only be done using synthetic graphs that have built-in community structure, power-law degree distribution, and other typical properties observed in complex networks. The standard and extensively used method for generating artificial networks is the LFR graph generator. Unfortunately, this model has some scalability limitations and it is challenging to analyze it theoretically. Finally, the mixing parameter $\mu$, the main parameter of the model guiding the strength of the communities, has a non-obvious interpretation and so can lead to unnaturally-defined networks. In this paper, we provide an alternative random graph model with community structure and power-law distribution for both degrees and community sizes, the Artificial Benchmark for Community Detection (ABCD). We show that the new model solves the three issues identified above and more. The conclusion is that these models produce comparable graphs but ABCD is fast, simple, and can be easily tuned to allow the user to make a smooth transition between the two extremes: pure (independent) communities and random graph with no community structure.