Properties and Performance of the ABCDe Random Graph Model with Community Structure

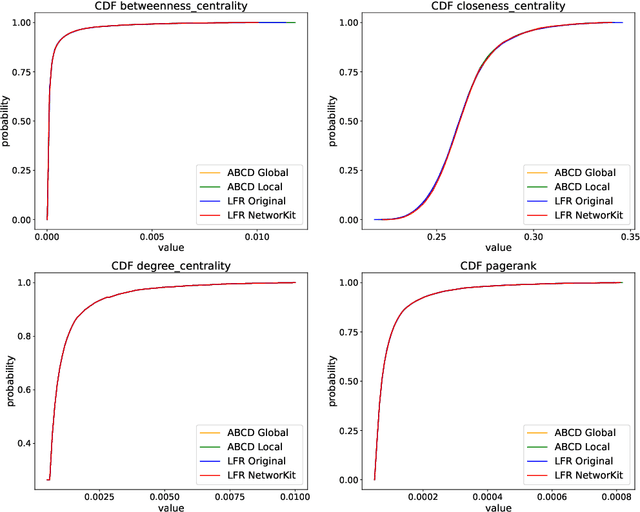
In this paper, we investigate properties and performance of synthetic random graph models with a built-in community structure. Such models are important for evaluating and tuning community detection algorithms that are unsupervised by nature. We propose a new implementation of the ABCD graph generator, ABCDe, that uses multiple-threading. We discuss the implementation details of the algorithm as well as compare it with both the previously available sequential version of the ABCD model and with the parallel implementation of the standard and extensively used LFR generator. We show that ABCDe is more than ten times faster and scales better than the parallel implementation of LFR provided in NetworKit. Moreover, the algorithm is not only faster but random graphs generated by ABCD have similar properties to the ones generated by the original LFR algorithm, while the parallelized NetworKit implementation of LFR produces graphs that have noticeably different characteristics.

Modularity of the ABCD Random Graph Model with Community Structure

The Artificial Benchmark for Community Detection (ABCD) graph is a random graph model with community structure and power-law distribution for both degrees and community sizes. The model generates graphs with similar properties as the well-known LFR one, and its main parameter $\xi$ can be tuned to mimic its counterpart in the LFR model, the mixing parameter $\mu$. In this paper, we investigate various theoretical asymptotic properties of the ABCD model. In particular, we analyze the modularity function, arguably, the most important graph property of networks in the context of community detection. Indeed, the modularity function is often used to measure the presence of community structure in networks. It is also used as a quality function in many community detection algorithms, including the widely used Louvain algorithm.