Controlling Overestimation Bias with Truncated Mixture of Continuous Distributional Quantile Critics

The overestimation bias is one of the major impediments to accurate off-policy learning. This paper investigates a novel way to alleviate the overestimation bias in a continuous control setting. Our method---Truncated Quantile Critics, TQC,---blends three ideas: distributional representation of a critic, truncation of critics prediction, and ensembling of multiple critics. Distributional representation and truncation allow for arbitrary granular overestimation control, while ensembling provides additional score improvements. TQC outperforms the current state of the art on all environments from the continuous control benchmark suite, demonstrating 25% improvement on the most challenging Humanoid environment.

YASENN: Explaining Neural Networks via Partitioning Activation Sequences

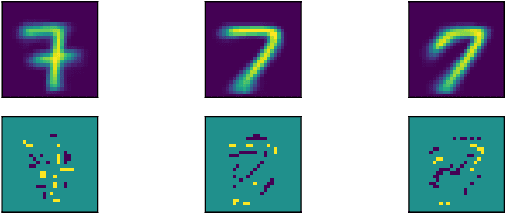
We introduce a novel approach to feed-forward neural network interpretation based on partitioning the space of sequences of neuron activations. In line with this approach, we propose a model-specific interpretation method, called YASENN. Our method inherits many advantages of model-agnostic distillation, such as an ability to focus on the particular input region and to express an explanation in terms of features different from those observed by a neural network. Moreover, examination of distillation error makes the method applicable to the problems with low tolerance to interpretation mistakes. Technically, YASENN distills the network with an ensemble of layer-wise gradient boosting decision trees and encodes the sequences of neuron activations with leaf indices. The finite number of unique codes induces a partitioning of the input space. Each partition may be described in a variety of ways, including examination of an interpretable model (e.g. a logistic regression or a decision tree) trained to discriminate between objects of those partitions. Our experiments provide an intuition behind the method and demonstrate revealed artifacts in neural network decision making.

Metropolis-Hastings view on variational inference and adversarial training

In this paper we propose to view the acceptance rate of the Metropolis-Hastings algorithm as a universal objective for learning to sample from target distribution -- given either as a set of samples or in the form of unnormalized density. This point of view unifies the goals of such approaches as Markov Chain Monte Carlo (MCMC), Generative Adversarial Networks (GANs), variational inference. To reveal the connection we derive the lower bound on the acceptance rate and treat it as the objective for learning explicit and implicit samplers. The form of the lower bound allows for doubly stochastic gradient optimization in case the target distribution factorizes (i.e. over data points). We empirically validate our approach on Bayesian inference for neural networks and generative models for images.