MolEdit: Knowledge Editing for Multimodal Molecule Language Models

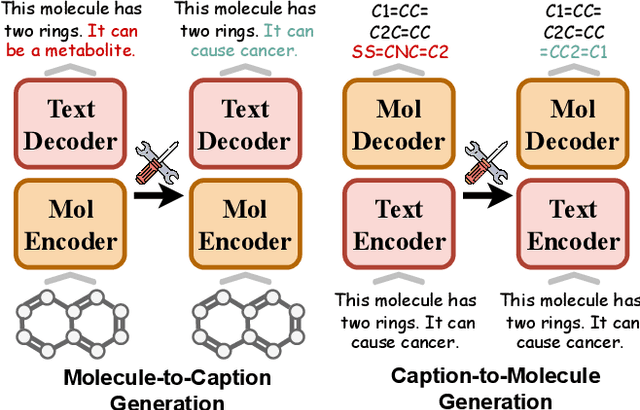
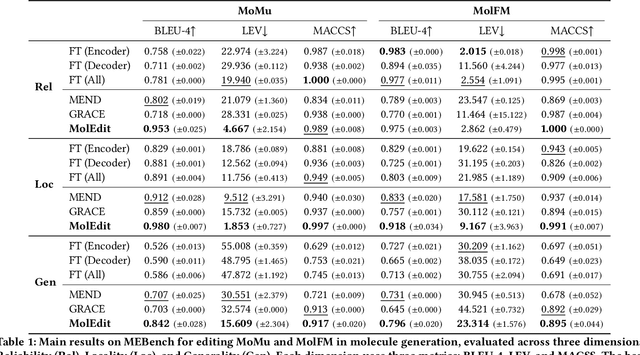
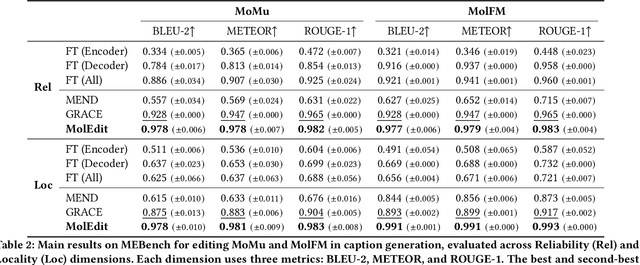
Understanding and continuously refining multimodal molecular knowledge is crucial for advancing biomedicine, chemistry, and materials science. Molecule language models (MoLMs) have become powerful tools in these domains, integrating structural representations (e.g., SMILES strings, molecular graphs) with rich contextual descriptions (e.g., physicochemical properties). However, MoLMs can encode and propagate inaccuracies due to outdated web-mined training corpora or malicious manipulation, jeopardizing downstream discovery pipelines. While knowledge editing has been explored for general-domain AI, its application to MoLMs remains uncharted, presenting unique challenges due to the multifaceted and interdependent nature of molecular knowledge. In this paper, we take the first step toward MoLM editing for two critical tasks: molecule-to-caption generation and caption-to-molecule generation. To address molecule-specific challenges, we propose MolEdit, a powerful framework that enables targeted modifications while preserving unrelated molecular knowledge. MolEdit combines a Multi-Expert Knowledge Adapter that routes edits to specialized experts for different molecular facets with an Expertise-Aware Editing Switcher that activates the adapters only when input closely matches the stored edits across all expertise, minimizing interference with unrelated knowledge. To systematically evaluate editing performance, we introduce MEBench, a comprehensive benchmark assessing multiple dimensions, including Reliability (accuracy of the editing), Locality (preservation of irrelevant knowledge), and Generality (robustness to reformed queries). Across extensive experiments on two popular MoLM backbones, MolEdit delivers up to 18.8% higher Reliability and 12.0% better Locality than baselines while maintaining efficiency. The code is available at: https://github.com/LzyFischer/MolEdit.

Graph Neural Networks Are More Than Filters: Revisiting and Benchmarking from A Spectral Perspective

Graph Neural Networks (GNNs) have achieved remarkable success in various graph-based learning tasks. While their performance is often attributed to the powerful neighborhood aggregation mechanism, recent studies suggest that other components such as non-linear layers may also significantly affecting how GNNs process the input graph data in the spectral domain. Such evidence challenges the prevalent opinion that neighborhood aggregation mechanisms dominate the behavioral characteristics of GNNs in the spectral domain. To demystify such a conflict, this paper introduces a comprehensive benchmark to measure and evaluate GNNs' capability in capturing and leveraging the information encoded in different frequency components of the input graph data. Specifically, we first conduct an exploratory study demonstrating that GNNs can flexibly yield outputs with diverse frequency components even when certain frequencies are absent or filtered out from the input graph data. We then formulate a novel research problem of measuring and benchmarking the performance of GNNs from a spectral perspective. To take an initial step towards a comprehensive benchmark, we design an evaluation protocol supported by comprehensive theoretical analysis. Finally, we introduce a comprehensive benchmark on real-world datasets, revealing insights that challenge prevalent opinions from a spectral perspective. We believe that our findings will open new avenues for future advancements in this area. Our implementations can be found at: https://github.com/yushundong/Spectral-benchmark.

Explaining Graph Neural Networks with Large Language Models: A Counterfactual Perspective for Molecular Property Prediction

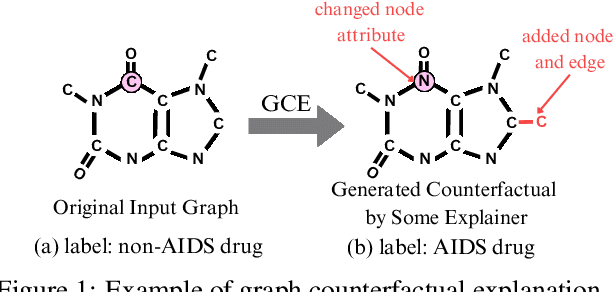
In recent years, Graph Neural Networks (GNNs) have become successful in molecular property prediction tasks such as toxicity analysis. However, due to the black-box nature of GNNs, their outputs can be concerning in high-stakes decision-making scenarios, e.g., drug discovery. Facing such an issue, Graph Counterfactual Explanation (GCE) has emerged as a promising approach to improve GNN transparency. However, current GCE methods usually fail to take domain-specific knowledge into consideration, which can result in outputs that are not easily comprehensible by humans. To address this challenge, we propose a novel GCE method, LLM-GCE, to unleash the power of large language models (LLMs) in explaining GNNs for molecular property prediction. Specifically, we utilize an autoencoder to generate the counterfactual graph topology from a set of counterfactual text pairs (CTPs) based on an input graph. Meanwhile, we also incorporate a CTP dynamic feedback module to mitigate LLM hallucination, which provides intermediate feedback derived from the generated counterfactuals as an attempt to give more faithful guidance. Extensive experiments demonstrate the superior performance of LLM-GCE. Our code is released on https://github.com/YinhanHe123/new\_LLM4GNNExplanation.

Bridging Graph Position Encodings for Transformers with Weighted Graph-Walking Automata

A current goal in the graph neural network literature is to enable transformers to operate on graph-structured data, given their success on language and vision tasks. Since the transformer's original sinusoidal positional encodings (PEs) are not applicable to graphs, recent work has focused on developing graph PEs, rooted in spectral graph theory or various spatial features of a graph. In this work, we introduce a new graph PE, Graph Automaton PE (GAPE), based on weighted graph-walking automata (a novel extension of graph-walking automata). We compare the performance of GAPE with other PE schemes on both machine translation and graph-structured tasks, and we show that it generalizes several other PEs. An additional contribution of this study is a theoretical and controlled experimental comparison of many recent PEs in graph transformers, independent of the use of edge features.