Questioning causality on sex, gender and COVID-19, and identifying bias in large-scale data-driven analyses: the Bias Priority Recommendations and Bias Catalog for Pandemics

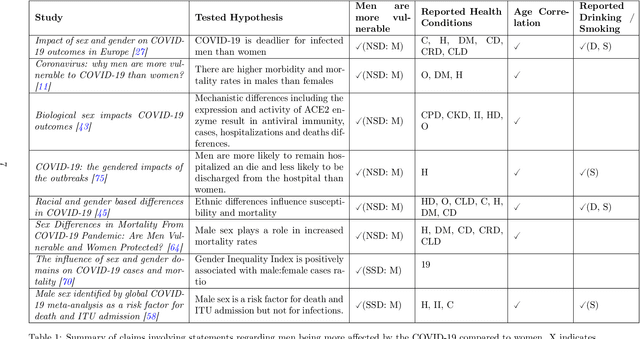
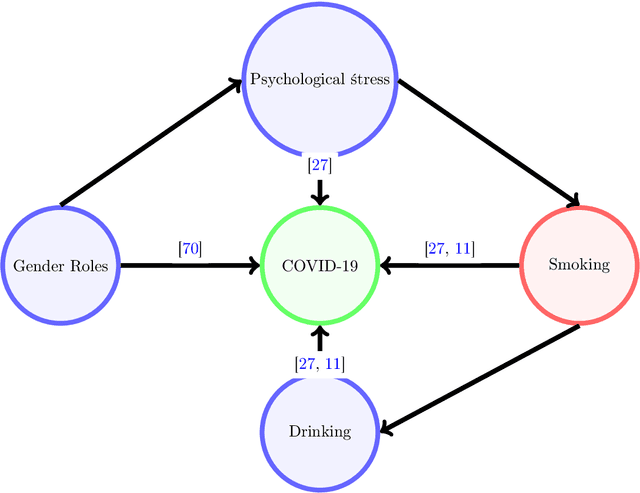
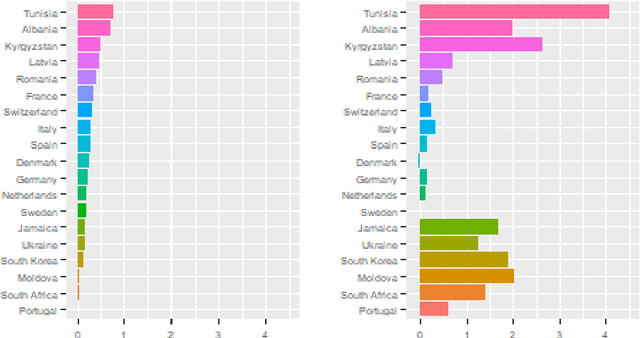
The COVID-19 pandemic has spurred a large amount of observational studies reporting linkages between the risk of developing severe COVID-19 or dying from it, and sex and gender. By reviewing a large body of related literature and conducting a fine grained analysis based on sex-disaggregated data of 61 countries spanning 5 continents, we discover several confounding factors that could possibly explain the supposed male vulnerability to COVID-19. We thus highlight the challenge of making causal claims based on available data, given the lack of statistical significance and potential existence of biases. Informed by our findings on potential variables acting as confounders, we contribute a broad overview on the issues bias, explainability and fairness entail in data-driven analyses. Thus, we outline a set of discriminatory policy consequences that could, based on such results, lead to unintended discrimination. To raise awareness on the dimensionality of such foreseen impacts, we have compiled an encyclopedia-like reference guide, the Bias Catalog for Pandemics (BCP), to provide definitions and emphasize realistic examples of bias in general, and within the COVID-19 pandemic context. These are categorized within a division of bias families and a 2-level priority scale, together with preventive steps. In addition, we facilitate the Bias Priority Recommendations on how to best use and apply this catalog, and provide guidelines in order to address real world research questions. The objective is to anticipate and avoid disparate impact and discrimination, by considering causality, explainability, bias and techniques to mitigate the latter. With these, we hope to 1) contribute to designing and conducting fair and equitable data-driven studies and research; and 2) interpret and draw meaningful and actionable conclusions from these.

Learning Functional Causal Models with Generative Neural Networks

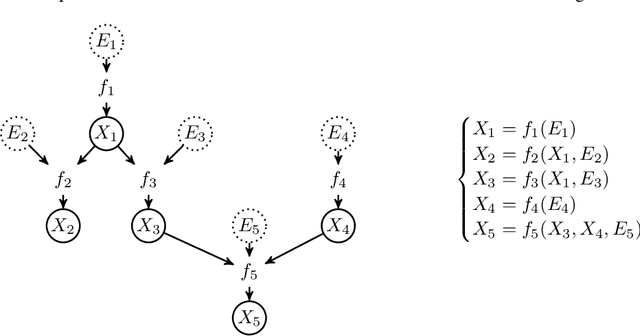
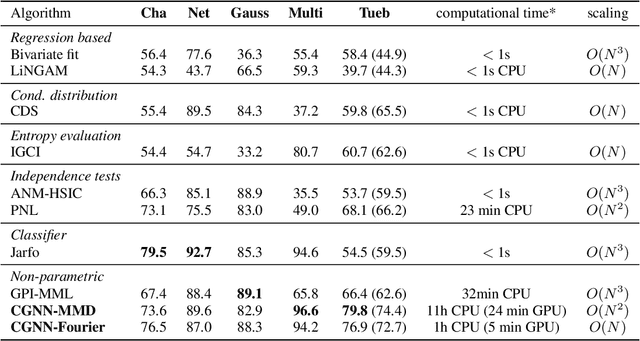
We introduce a new approach to functional causal modeling from observational data. The approach, called Causal Generative Neural Networks (CGNN), leverages the power of neural networks to learn a generative model of the joint distribution of the observed variables, by minimizing the Maximum Mean Discrepancy between generated and observed data. An approximate learning criterion is proposed to scale the computational cost of the approach to linear complexity in the number of observations. The performance of CGNN is studied throughout three experiments. First, we apply CGNN to the problem of cause-effect inference, where two CGNNs model $P(Y|X,\textrm{noise})$ and $P(X|Y,\textrm{noise})$ identify the best causal hypothesis out of $X\rightarrow Y$ and $Y\rightarrow X$. Second, CGNN is applied to the problem of identifying v-structures and conditional independences. Third, we apply CGNN to problem of multivariate functional causal modeling: given a skeleton describing the dependences in a set of random variables $\{X_1, \ldots, X_d\}$, CGNN orients the edges in the skeleton to uncover the directed acyclic causal graph describing the causal structure of the random variables. On all three tasks, CGNN is extensively assessed on both artificial and real-world data, comparing favorably to the state-of-the-art. Finally, we extend CGNN to handle the case of confounders, where latent variables are involved in the overall causal model.