MLGWSC-1: The first Machine Learning Gravitational-Wave Search Mock Data Challenge

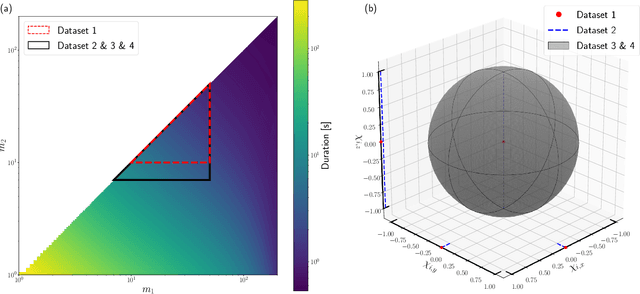
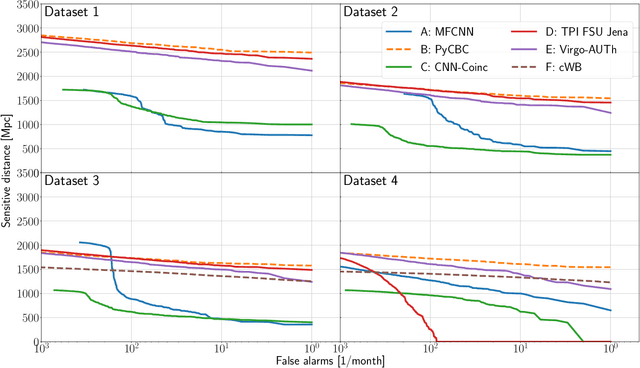
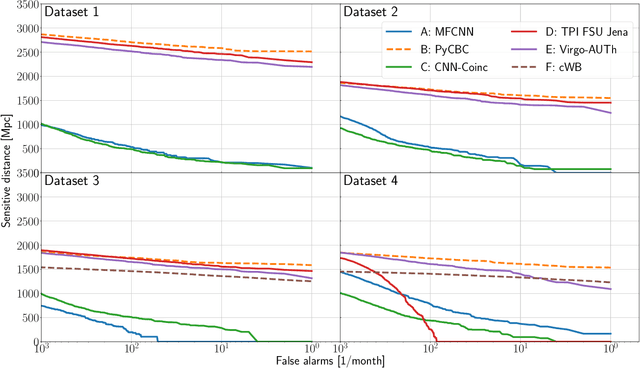
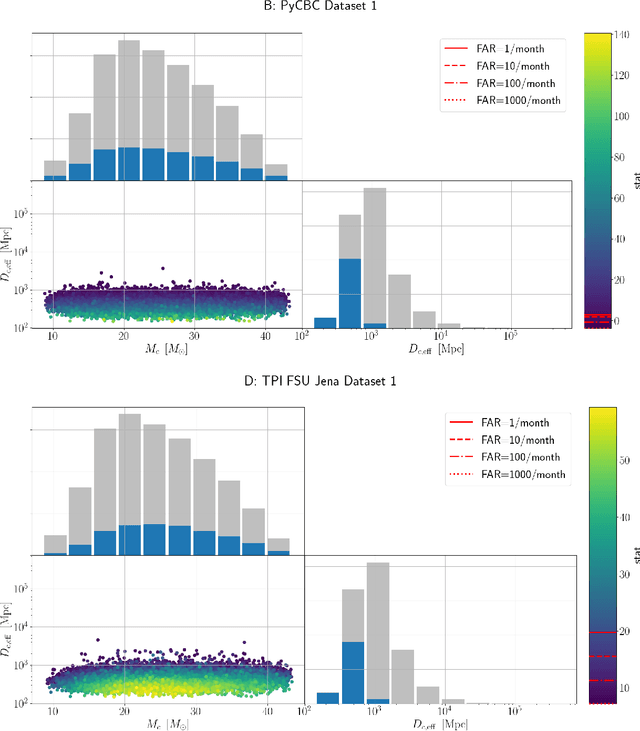
We present the results of the first Machine Learning Gravitational-Wave Search Mock Data Challenge (MLGWSC-1). For this challenge, participating groups had to identify gravitational-wave signals from binary black hole mergers of increasing complexity and duration embedded in progressively more realistic noise. The final of the 4 provided datasets contained real noise from the O3a observing run and signals up to a duration of 20 seconds with the inclusion of precession effects and higher order modes. We present the average sensitivity distance and runtime for the 6 entered algorithms derived from 1 month of test data unknown to the participants prior to submission. Of these, 4 are machine learning algorithms. We find that the best machine learning based algorithms are able to achieve up to 95% of the sensitive distance of matched-filtering based production analyses for simulated Gaussian noise at a false-alarm rate (FAR) of one per month. In contrast, for real noise, the leading machine learning search achieved 70%. For higher FARs the differences in sensitive distance shrink to the point where select machine learning submissions outperform traditional search algorithms at FARs $\geq 200$ per month on some datasets. Our results show that current machine learning search algorithms may already be sensitive enough in limited parameter regions to be useful for some production settings. To improve the state-of-the-art, machine learning algorithms need to reduce the false-alarm rates at which they are capable of detecting signals and extend their validity to regions of parameter space where modeled searches are computationally expensive to run. Based on our findings we compile a list of research areas that we believe are the most important to elevate machine learning searches to an invaluable tool in gravitational-wave signal detection.

Deep Residual Error and Bag-of-Tricks Learning for Gravitational Wave Surrogate Modeling

Deep learning methods have been employed in gravitational-wave astronomy to accelerate the construction of surrogate waveforms for the inspiral of spin-aligned black hole binaries, among other applications. We demonstrate, that the residual error of an artificial neural network that models the coefficients of the surrogate waveform expansion (especially those of the phase of the waveform) has sufficient structure to be learnable by a second network. Adding this second network, we were able to reduce the maximum mismatch for waveforms in a validation set by more than an order of magnitude. We also explored several other ideas for improving the accuracy of the surrogate model, such as the exploitation of similarities between waveforms, the augmentation of the training set, the dissection of the input space, using dedicated networks per output coefficient and output augmentation. In several cases, small improvements can be observed, but the most significant improvement still comes from the addition of a second network that models the residual error. Since the residual error for more general surrogate waveform models (when e.g. eccentricity is included) may also have a specific structure, one can expect our method to be applicable to cases where the gain in accuracy could lead to significant gains in computational time.

Autoencoder-driven Spiral Representation Learning for Gravitational Wave Surrogate Modelling

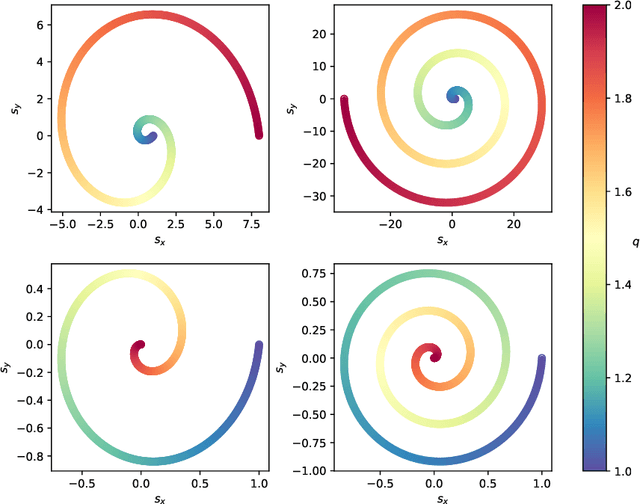
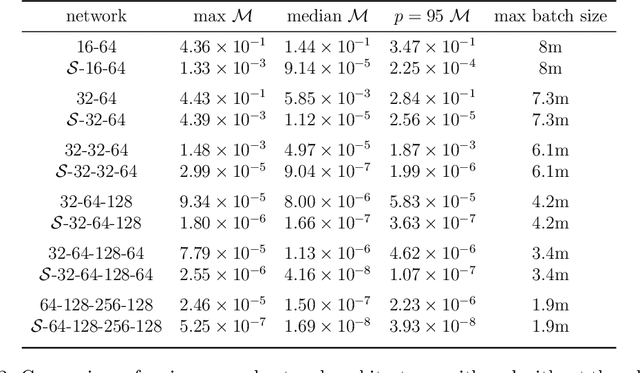
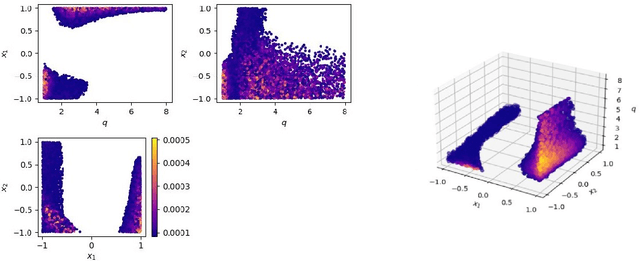
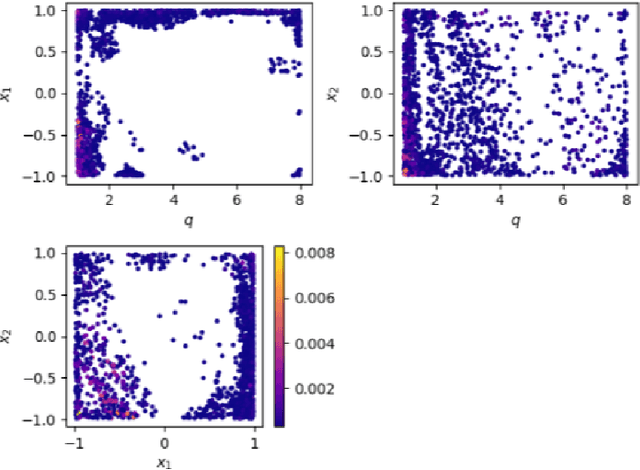
Recently, artificial neural networks have been gaining momentum in the field of gravitational wave astronomy, for example in surrogate modelling of computationally expensive waveform models for binary black hole inspiral and merger. Surrogate modelling yields fast and accurate approximations of gravitational waves and neural networks have been used in the final step of interpolating the coefficients of the surrogate model for arbitrary waveforms outside the training sample. We investigate the existence of underlying structures in the empirical interpolation coefficients using autoencoders. We demonstrate that when the coefficient space is compressed to only two dimensions, a spiral structure appears, wherein the spiral angle is linearly related to the mass ratio. Based on this finding, we design a spiral module with learnable parameters, that is used as the first layer in a neural network, which learns to map the input space to the coefficients. The spiral module is evaluated on multiple neural network architectures and consistently achieves better speed-accuracy trade-off than baseline models. A thorough experimental study is conducted and the final result is a surrogate model which can evaluate millions of input parameters in a single forward pass in under 1ms on a desktop GPU, while the mismatch between the corresponding generated waveforms and the ground-truth waveforms is better than the compared baseline methods. We anticipate the existence of analogous underlying structures and corresponding computational gains also in the case of spinning black hole binaries.