Combining Machine Learning with Recurrence Analysis for resonance detection

The width of a resonance in a nearly integrable system, i.e. in a non-integrable system where chaotic motion is still not prominent, can tell us how a perturbation parameter is driving the system away from integrability. Although the tool that we are presenting here can be used is quite generic and can be used in a variety of systems, our particular interest lies in binary compact object systems known as extreme mass ratio inspirals (EMRIs). In an EMRI a lighter compact object, like a black hole or a neutron star, inspirals into a supermassive black hole due to gravitational radiation reaction. During this inspiral the lighter object crosses resonances, which are still not very well modeled. Measuring the width of resonances in EMRI models allows us to estimate the importance of each perturbation parameter able to drive the system away from resonances and decide whether its impact should be included in EMRI waveform modeling or not. To tackle this issue in our study we show first that recurrence quantifiers of orbits carry imprints of resonant behavior, regardless of the system's dimensionality. As a next step, we apply a long short-term memory machine learning architecture to automate the resonance detection procedure. Our analysis is developed on a simple standard map and gradually we extend it to more complicated systems until finally we employ it in a generic deformed Kerr spacetime known in the literature as the Johannsen-Psaltis spacetime.

Convolutional Neural Networks for signal detection in real LIGO data

Searching the data of gravitational-wave detectors for signals from compact binary mergers is a computationally demanding task. Recently, machine learning algorithms have been proposed to address current and future challenges. However, the results of these publications often differ greatly due to differing choices in the evaluation procedure. The Machine Learning Gravitational-Wave Search Challenge was organized to resolve these issues and produce a unified framework for machine-learning search evaluation. Six teams submitted contributions, four of which are based on machine learning methods and two are state-of-the-art production analyses. This paper describes the submission from the team TPI FSU Jena and its updated variant. We also apply our algorithm to real O3b data and recover the relevant events of the GWTC-3 catalog.

MLGWSC-1: The first Machine Learning Gravitational-Wave Search Mock Data Challenge

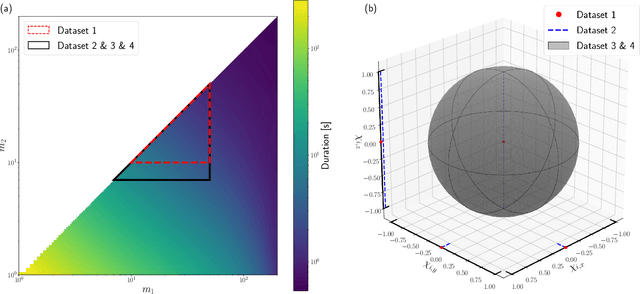
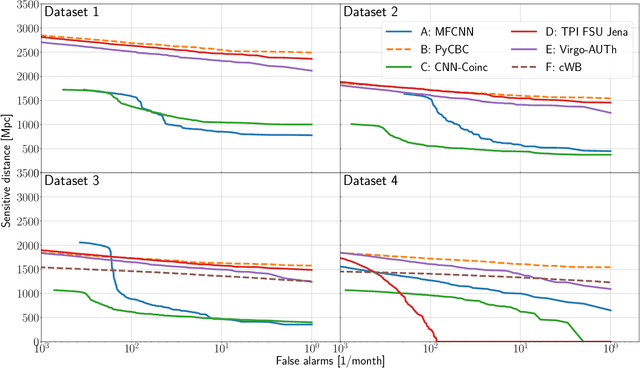
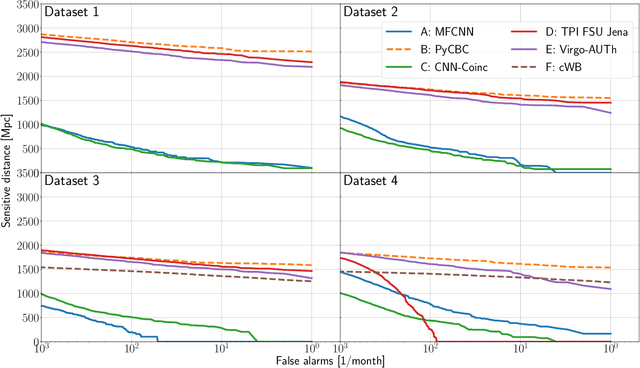
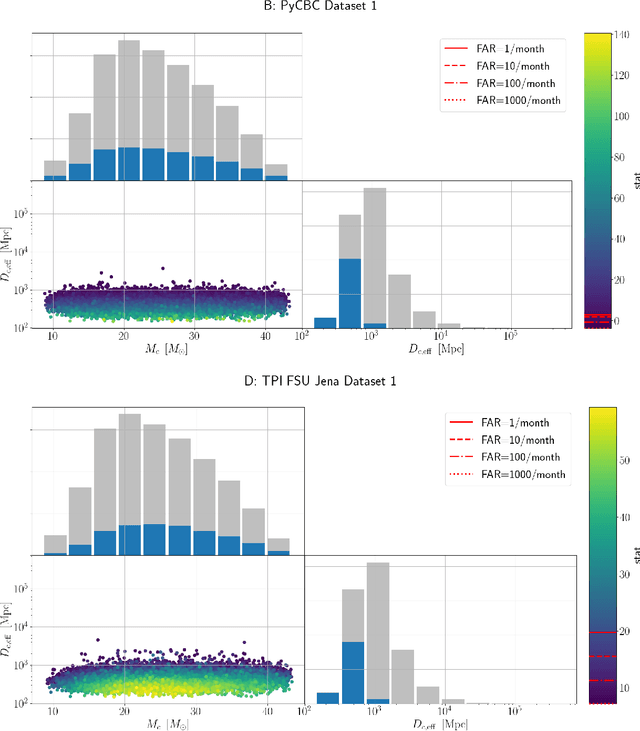
We present the results of the first Machine Learning Gravitational-Wave Search Mock Data Challenge (MLGWSC-1). For this challenge, participating groups had to identify gravitational-wave signals from binary black hole mergers of increasing complexity and duration embedded in progressively more realistic noise. The final of the 4 provided datasets contained real noise from the O3a observing run and signals up to a duration of 20 seconds with the inclusion of precession effects and higher order modes. We present the average sensitivity distance and runtime for the 6 entered algorithms derived from 1 month of test data unknown to the participants prior to submission. Of these, 4 are machine learning algorithms. We find that the best machine learning based algorithms are able to achieve up to 95% of the sensitive distance of matched-filtering based production analyses for simulated Gaussian noise at a false-alarm rate (FAR) of one per month. In contrast, for real noise, the leading machine learning search achieved 70%. For higher FARs the differences in sensitive distance shrink to the point where select machine learning submissions outperform traditional search algorithms at FARs $\geq 200$ per month on some datasets. Our results show that current machine learning search algorithms may already be sensitive enough in limited parameter regions to be useful for some production settings. To improve the state-of-the-art, machine learning algorithms need to reduce the false-alarm rates at which they are capable of detecting signals and extend their validity to regions of parameter space where modeled searches are computationally expensive to run. Based on our findings we compile a list of research areas that we believe are the most important to elevate machine learning searches to an invaluable tool in gravitational-wave signal detection.

Training Strategies for Deep Learning Gravitational-Wave Searches

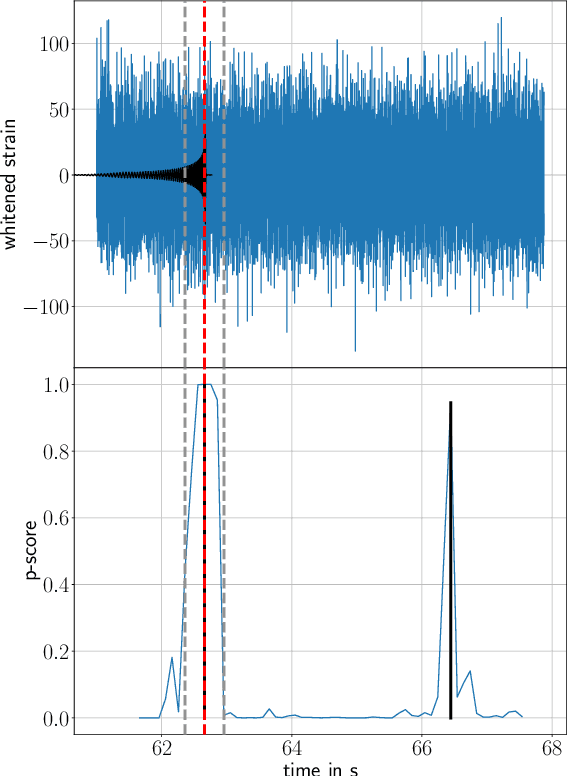
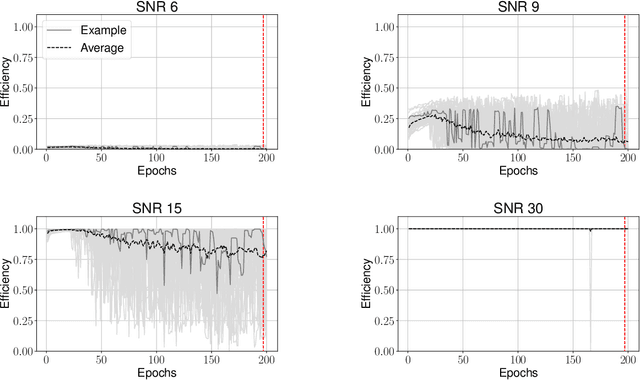
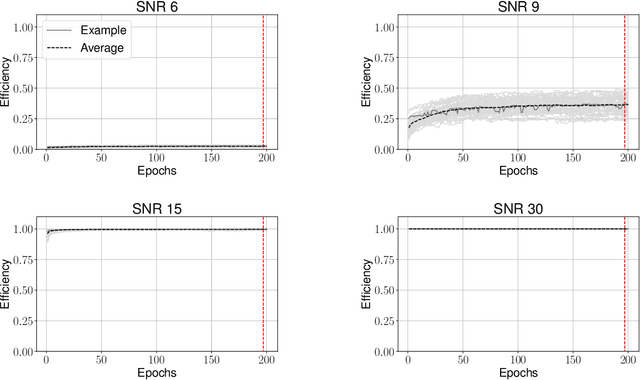
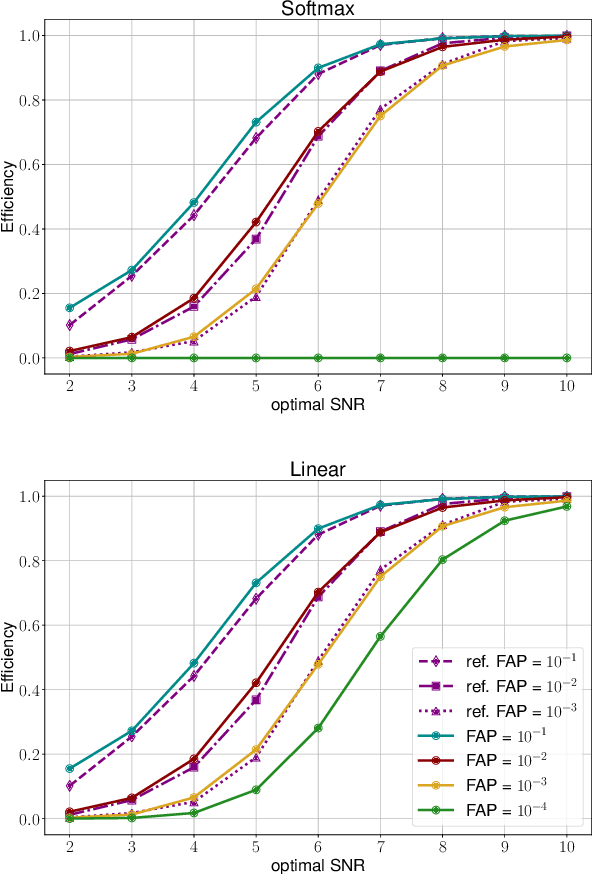
Compact binary systems emit gravitational radiation which is potentially detectable by current Earth bound detectors. Extracting these signals from the instruments' background noise is a complex problem and the computational cost of most current searches depends on the complexity of the source model. Deep learning may be capable of finding signals where current algorithms hit computational limits. Here we restrict our analysis to signals from non-spinning binary black holes and systematically test different strategies by which training data is presented to the networks. To assess the impact of the training strategies, we re-analyze the first published networks and directly compare them to an equivalent matched-filter search. We find that the deep learning algorithms can generalize low signal-to-noise ratio (SNR) signals to high SNR ones but not vice versa. As such, it is not beneficial to provide high SNR signals during training, and fastest convergence is achieved when low SNR samples are provided early on. During testing we found that the networks are sometimes unable to recover any signals when a false alarm probability $<10^{-3}$ is required. We resolve this restriction by applying a modification we call unbounded Softmax replacement (USR) after training. With this alteration we find that the machine learning search retains $\geq 97.5\%$ of the sensitivity of the matched-filter search down to a false-alarm rate of 1 per month.