Ozan Yildiz
Fair Distributions from Biased Samples: A Maximum Entropy Optimization Framework
Jun 05, 2019



Abstract:One reason for the emergence of bias in AI systems is biased data -- datasets that may not be true representations of the underlying distributions -- and may over or under-represent groups with respect to protected attributes such as gender or race. We consider the problem of correcting such biases and learning distributions that are "fair", with respect to measures such as proportional representation and statistical parity, from the given samples. Our approach is based on a novel formulation of the problem of learning a fair distribution as a maximum entropy optimization problem with a given expectation vector and a prior distribution. Technically, our main contributions are: (1) a new second-order method to compute the (dual of the) maximum entropy distribution over an exponentially-sized discrete domain that turns out to be faster than previous methods, and (2) methods to construct prior distributions and expectation vectors that provably guarantee that the learned distributions satisfy a wide class of fairness criteria. Our results also come with quantitative bounds on the total variation distance between the empirical distribution obtained from the samples and the learned fair distribution. Our experimental results include testing our approach on the COMPAS dataset and showing that the fair distributions not only improve disparate impact values but when used to train classifiers only incur a small loss of accuracy.
Energy Saving Additive Neural Network
Feb 09, 2017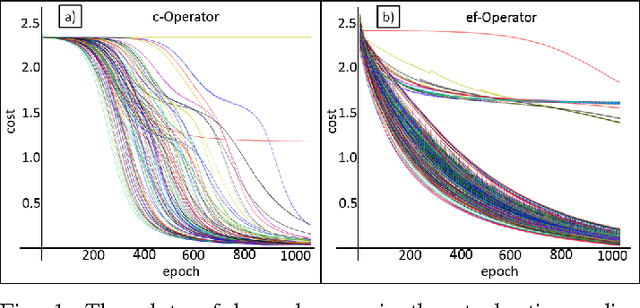
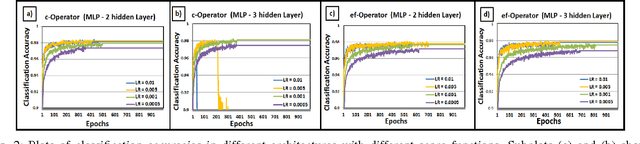
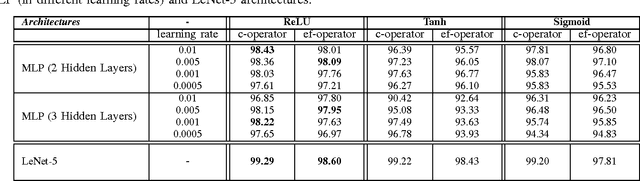
Abstract:In recent years, machine learning techniques based on neural networks for mobile computing become increasingly popular. Classical multi-layer neural networks require matrix multiplications at each stage. Multiplication operation is not an energy efficient operation and consequently it drains the battery of the mobile device. In this paper, we propose a new energy efficient neural network with the universal approximation property over space of Lebesgue integrable functions. This network, called, additive neural network, is very suitable for mobile computing. The neural structure is based on a novel vector product definition, called ef-operator, that permits a multiplier-free implementation. In ef-operation, the "product" of two real numbers is defined as the sum of their absolute values, with the sign determined by the sign of the product of the numbers. This "product" is used to construct a vector product in $R^N$. The vector product induces the $l_1$ norm. The proposed additive neural network successfully solves the XOR problem. The experiments on MNIST dataset show that the classification performances of the proposed additive neural networks are very similar to the corresponding multi-layer perceptron and convolutional neural networks (LeNet).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge