Polarization Multiplexed Diffractive Computing: All-Optical Implementation of a Group of Linear Transformations Through a Polarization-Encoded Diffractive Network

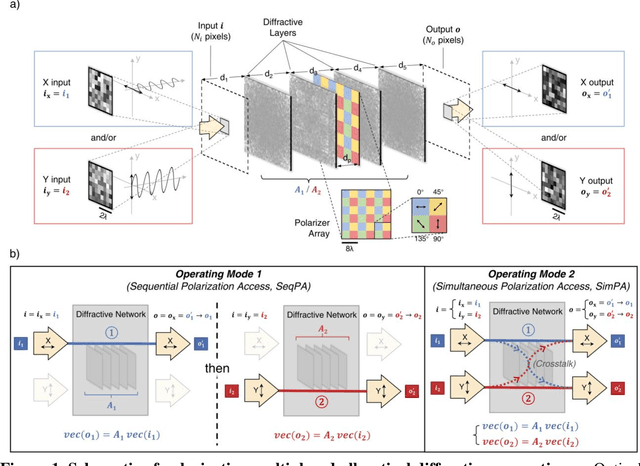
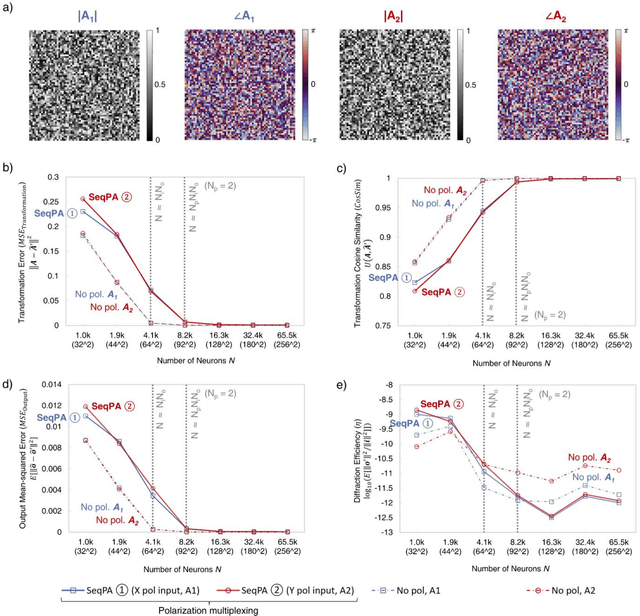
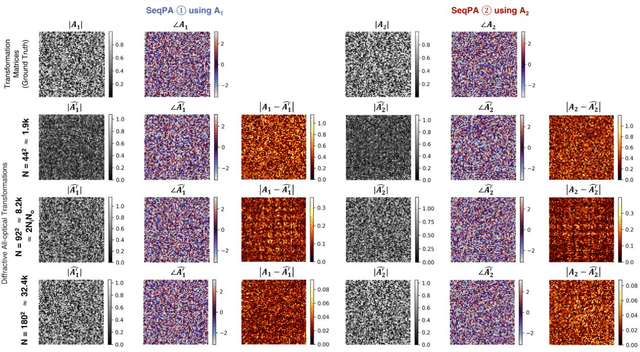
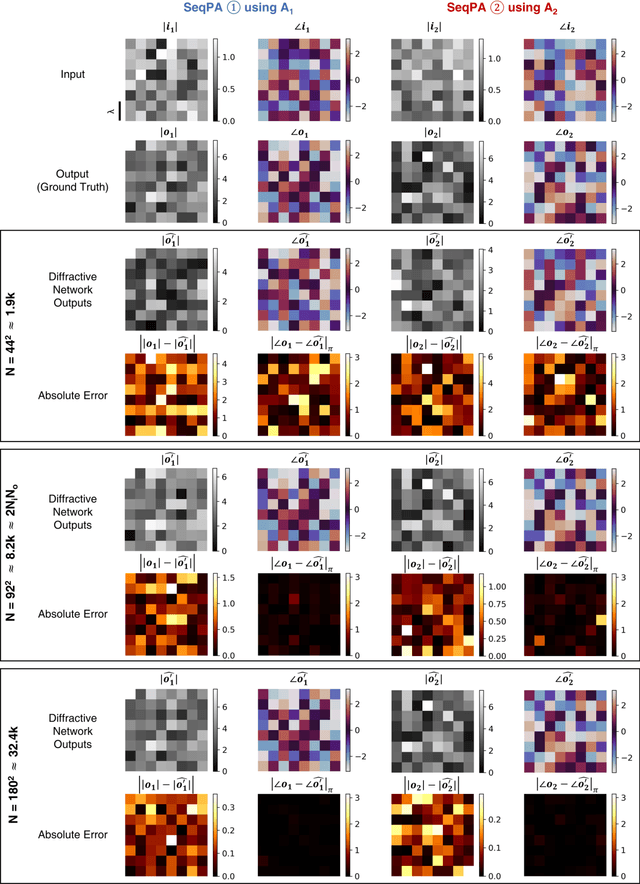
Research on optical computing has recently attracted significant attention due to the transformative advances in machine learning. Among different approaches, diffractive optical networks composed of spatially-engineered transmissive surfaces have been demonstrated for all-optical statistical inference and performing arbitrary linear transformations using passive, free-space optical layers. Here, we introduce a polarization multiplexed diffractive processor to all-optically perform multiple, arbitrarily-selected linear transformations through a single diffractive network trained using deep learning. In this framework, an array of pre-selected linear polarizers is positioned between trainable transmissive diffractive materials that are isotropic, and different target linear transformations (complex-valued) are uniquely assigned to different combinations of input/output polarization states. The transmission layers of this polarization multiplexed diffractive network are trained and optimized via deep learning and error-backpropagation by using thousands of examples of the input/output fields corresponding to each one of the complex-valued linear transformations assigned to different input/output polarization combinations. Our results and analysis reveal that a single diffractive network can successfully approximate and all-optically implement a group of arbitrarily-selected target transformations with a negligible error when the number of trainable diffractive features/neurons (N) approaches N_p x N_i x N_o, where N_i and N_o represent the number of pixels at the input and output fields-of-view, respectively, and N_p refers to the number of unique linear transformations assigned to different input/output polarization combinations. This polarization-multiplexed all-optical diffractive processor can find various applications in optical computing and polarization-based machine vision tasks.

All-Optical Synthesis of an Arbitrary Linear Transformation Using Diffractive Surfaces

We report the design of diffractive surfaces to all-optically perform arbitrary complex-valued linear transformations between an input (N_i) and output (N_o), where N_i and N_o represent the number of pixels at the input and output fields-of-view (FOVs), respectively. First, we consider a single diffractive surface and use a matrix pseudoinverse-based method to determine the complex-valued transmission coefficients of the diffractive features/neurons to all-optically perform a desired/target linear transformation. In addition to this data-free design approach, we also consider a deep learning-based design method to optimize the transmission coefficients of diffractive surfaces by using examples of input/output fields corresponding to the target transformation. We compared the all-optical transformation errors and diffraction efficiencies achieved using data-free designs as well as data-driven (deep learning-based) diffractive designs to all-optically perform (i) arbitrarily-chosen complex-valued transformations including unitary, nonunitary and noninvertible transforms, (ii) 2D discrete Fourier transformation, (iii) arbitrary 2D permutation operations, and (iv) high-pass filtered coherent imaging. Our analyses reveal that if the total number (N) of spatially-engineered diffractive features/neurons is N_i x N_o or larger, both design methods succeed in all-optical implementation of the target transformation, achieving negligible error. However, compared to data-free designs, deep learning-based diffractive designs are found to achieve significantly larger diffraction efficiencies for a given N and their all-optical transformations are more accurate for N < N_i x N_o. These conclusions are generally applicable to various optical processors that employ spatially-engineered diffractive surfaces.

All-Optical Information Processing Capacity of Diffractive Surfaces

Precise engineering of materials and surfaces has been at the heart of some of the recent advances in optics and photonics. These advances around the engineering of materials with new functionalities have also opened up exciting avenues for designing trainable surfaces that can perform computation and machine learning tasks through light-matter interaction and diffraction. Here, we analyze the information processing capacity of coherent optical networks formed by diffractive surfaces that are trained to perform an all-optical computational task between a given input and output field-of-view. We prove that the dimensionality of the all-optical solution space covering the complex-valued transformations between the input and output fields-of-view is linearly proportional to the number of diffractive surfaces within the optical network, up to a limit that is dictated by the extent of the input and output fields-of-view. Deeper diffractive networks that are composed of larger numbers of trainable surfaces can cover a higher dimensional subspace of the complex-valued linear transformations between a larger input field-of-view and a larger output field-of-view, and exhibit depth advantages in terms of their statistical inference, learning and generalization capabilities for different image classification tasks, when compared with a single trainable diffractive surface. These analyses and conclusions are broadly applicable to various forms of diffractive surfaces, including e.g., plasmonic and/or dielectric-based metasurfaces and flat optics that can be used to form all-optical processors.