Ondrej Kuzelka
First-Order Context-Specific Likelihood Weighting in Hybrid Probabilistic Logic Programs
Jan 26, 2022
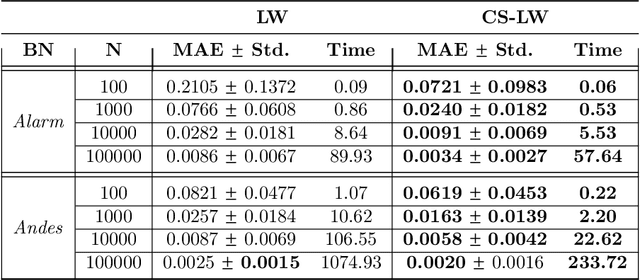

Abstract:Statistical relational AI and probabilistic logic programming have so far mostly focused on discrete probabilistic models. The reasons for this is that one needs to provide constructs to succinctly model the independencies in such models, and also provide efficient inference. Three types of independencies are important to represent and exploit for scalable inference in hybrid models: conditional independencies elegantly modeled in Bayesian networks, context-specific independencies naturally represented by logical rules, and independencies amongst attributes of related objects in relational models succinctly expressed by combining rules. This paper introduces a hybrid probabilistic logic programming language, DC#, which integrates distributional clauses' syntax and semantics principles of Bayesian logic programs. It represents the three types of independencies qualitatively. More importantly, we also introduce the scalable inference algorithm FO-CS-LW for DC#. FO-CS-LW is a first-order extension of the context-specific likelihood weighting algorithm (CS-LW), a novel sampling method that exploits conditional independencies and context-specific independencies in ground models. The FO-CS-LW algorithm upgrades CS-LW with unification and combining rules to the first-order case.
Learning with Molecules beyond Graph Neural Networks
Nov 06, 2020
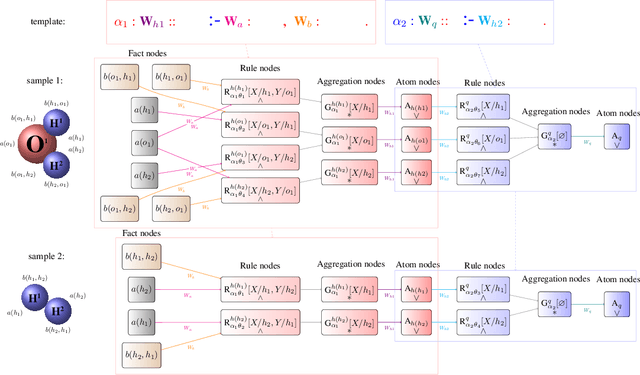
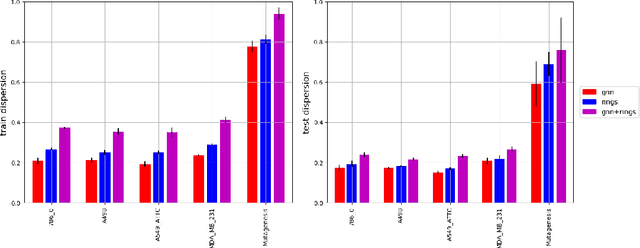
Abstract:We demonstrate a deep learning framework which is inherently based in the highly expressive language of relational logic, enabling to, among other things, capture arbitrarily complex graph structures. We show how Graph Neural Networks and similar models can be easily covered in the framework by specifying the underlying propagation rules in the relational logic. The declarative nature of the used language then allows to easily modify and extend the propagation schemes into complex structures, such as the molecular rings which we choose for a short demonstration in this paper.
Beyond Graph Neural Networks with Lifted Relational Neural Networks
Jul 13, 2020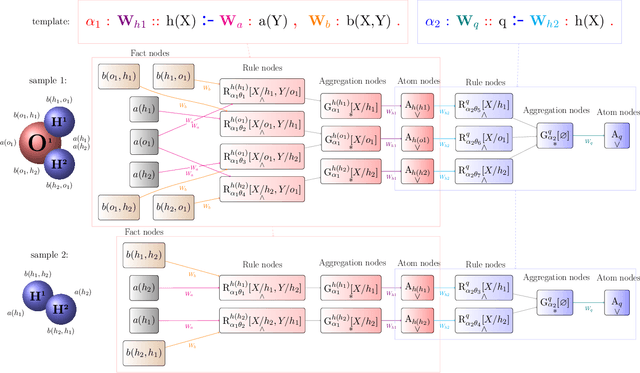


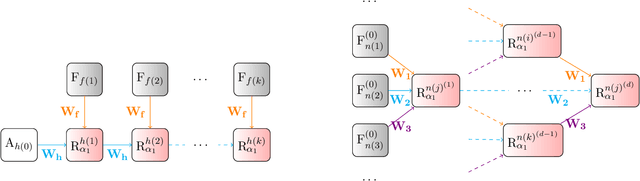
Abstract:We demonstrate a declarative differentiable programming framework based on the language of Lifted Relational Neural Networks, where small parameterized logic programs are used to encode relational learning scenarios. When presented with relational data, such as various forms of graphs, the program interpreter dynamically unfolds differentiable computational graphs to be used for the program parameter optimization by standard means. Following from the used declarative Datalog abstraction, this results into compact and elegant learning programs, in contrast with the existing procedural approaches operating directly on the computational graph level. We illustrate how this idea can be used for an efficient encoding of a diverse range of existing advanced neural architectures, with a particular focus on Graph Neural Networks (GNNs). Additionally, we show how the contemporary GNN models can be easily extended towards higher relational expressiveness. In the experiments, we demonstrate correctness and computation efficiency through comparison against specialized GNN deep learning frameworks, while shedding some light on the learning performance of existing GNN models.
Weighted First-Order Model Counting in the Two-Variable Fragment With Counting Quantifiers
Jul 10, 2020



Abstract:It is known due to the work of Van den Broeck et al [KR, 2014] that weighted first-order model counting (WFOMC) in the two-variable fragment of first-order logic can be solved in time polynomial in the number of domain elements. In this paper we extend this result to the two-variable fragment with counting quantifiers.
Lifted Inference in 2-Variable Markov Logic Networks with Function and Cardinality Constraints Using Discrete Fourier Transform
Jun 04, 2020
Abstract:In this paper we show that inference in 2-variable Markov logic networks (MLNs) with cardinality and function constraints is domain-liftable. To obtain this result we use existing domain-lifted algorithms for weighted first-order model counting (Van den Broeck et al, KR 2014) together with discrete Fourier transform of certain distributions associated to MLNs.
Markov Logic Networks with Complex Weights: Expressivity, Liftability and Fourier Transforms
Feb 24, 2020

Abstract:We study expressivity of Markov logic networks (MLNs). We introduce complex MLNs, which use complex-valued weights, and we show that, unlike standard MLNs with real-valued weights, complex MLNs are fully expressive. We then observe that discrete Fourier transform can be computed using weighted first order model counting (WFOMC) with complex weights and use this observation to design an algorithm for computing relational marginal polytopes which needs substantially less calls to a WFOMC oracle than a recent algorithm.
Approximate Weighted First-Order Model Counting: Exploiting Fast Approximate Model Counters and Symmetry
Jan 15, 2020
Abstract:We study the symmetric weighted first-order model counting task and present ApproxWFOMC, a novel anytime method for efficiently bounding the weighted first-order model count in the presence of an unweighted first-order model counting oracle. The algorithm has applications to inference in a variety of first-order probabilistic representations, such as Markov logic networks and probabilistic logic programs. Crucially for many applications, we make no assumptions on the form of the input sentence. Instead, our algorithm makes use of the symmetry inherent in the problem by imposing cardinality constraints on the number of possible true groundings of a sentence's literals. Realising the first-order model counting oracle in practice using the approximate hashing-based model counter ApproxMC3, we show how our algorithm outperforms existing approximate and exact techniques for inference in first-order probabilistic models. We additionally provide PAC guarantees on the generated bounds.
Domain-Liftability of Relational Marginal Polytopes
Jan 15, 2020Abstract:We study computational aspects of relational marginal polytopes which are statistical relational learning counterparts of marginal polytopes, well-known from probabilistic graphical models. Here, given some first-order logic formula, we can define its relational marginal statistic to be the fraction of groundings that make this formula true in a given possible world. For a list of first-order logic formulas, the relational marginal polytope is the set of all points that correspond to the expected values of the relational marginal statistics that are realizable. In this paper, we study the following two problems: (i) Do domain-liftability results for the partition functions of Markov logic networks (MLNs) carry over to the problem of relational marginal polytope construction? (ii) Is the relational marginal polytope containment problem hard under some plausible complexity-theoretic assumptions? Our positive results have consequences for lifted weight learning of MLNs. In particular, we show that weight learning of MLNs is domain-liftable whenever the computation of the partition function of the respective MLNs is domain-liftable (this result has not been rigorously proven before).
Lifted Weight Learning of Markov Logic Networks Revisited
Mar 07, 2019Abstract:We study lifted weight learning of Markov logic networks. We show that there is an algorithm for maximum-likelihood learning of 2-variable Markov logic networks which runs in time polynomial in the domain size. Our results are based on existing lifted-inference algorithms and recent algorithmic results on computing maximum entropy distributions.
Quantified Markov Logic Networks
Aug 21, 2018Abstract:Markov Logic Networks (MLNs) are well-suited for expressing statistics such as "with high probability a smoker knows another smoker" but not for expressing statements such as "there is a smoker who knows most other smokers", which is necessary for modeling, e.g. influencers in social networks. To overcome this shortcoming, we study quantified MLNs which generalize MLNs by introducing statistical universal quantifiers, allowing to express also the latter type of statistics in a principled way. Our main technical contribution is to show that the standard reasoning tasks in quantified MLNs, maximum a posteriori and marginal inference, can be reduced to their respective MLN counterparts in polynomial time.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge