Learning with Molecules beyond Graph Neural Networks

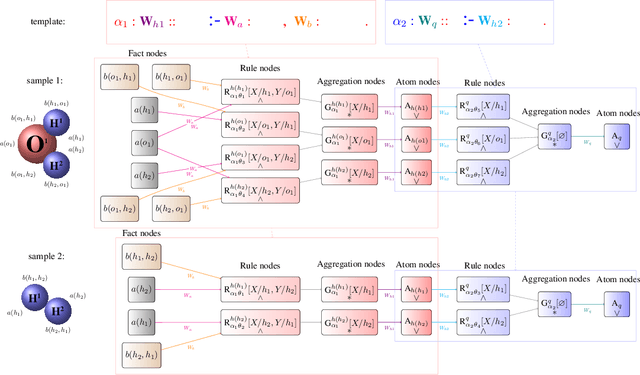
We demonstrate a deep learning framework which is inherently based in the highly expressive language of relational logic, enabling to, among other things, capture arbitrarily complex graph structures. We show how Graph Neural Networks and similar models can be easily covered in the framework by specifying the underlying propagation rules in the relational logic. The declarative nature of the used language then allows to easily modify and extend the propagation schemes into complex structures, such as the molecular rings which we choose for a short demonstration in this paper.

Beyond Graph Neural Networks with Lifted Relational Neural Networks

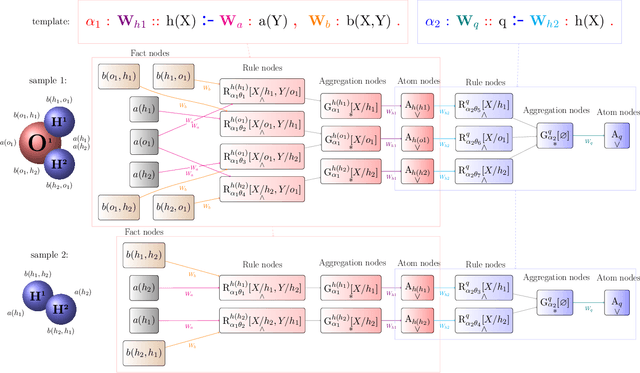
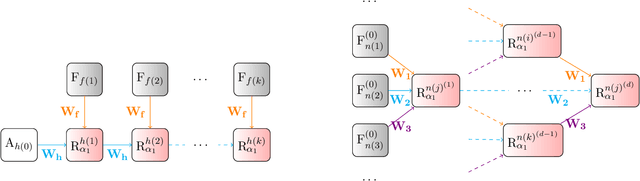
We demonstrate a declarative differentiable programming framework based on the language of Lifted Relational Neural Networks, where small parameterized logic programs are used to encode relational learning scenarios. When presented with relational data, such as various forms of graphs, the program interpreter dynamically unfolds differentiable computational graphs to be used for the program parameter optimization by standard means. Following from the used declarative Datalog abstraction, this results into compact and elegant learning programs, in contrast with the existing procedural approaches operating directly on the computational graph level. We illustrate how this idea can be used for an efficient encoding of a diverse range of existing advanced neural architectures, with a particular focus on Graph Neural Networks (GNNs). Additionally, we show how the contemporary GNN models can be easily extended towards higher relational expressiveness. In the experiments, we demonstrate correctness and computation efficiency through comparison against specialized GNN deep learning frameworks, while shedding some light on the learning performance of existing GNN models.

Lossless Compression of Structured Convolutional Models via Lifting

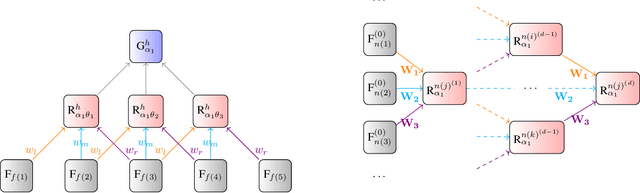
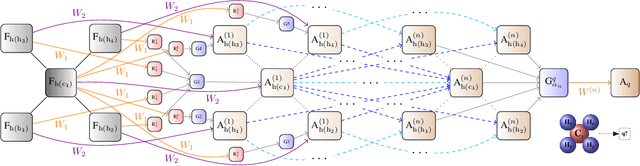
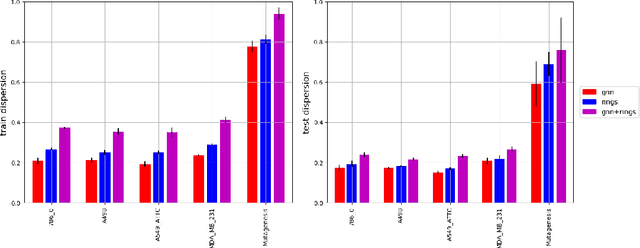
Lifting is an efficient technique to scale up graphical models generalized to relational domains by exploiting the underlying symmetries. Concurrently, neural models are continuously expanding from grid-like tensor data into structured representations, such as various attributed graphs and relational databases. To address the irregular structure of the data, the models typically extrapolate on the idea of convolution, effectively introducing parameter sharing in their, dynamically unfolded, computation graphs. The computation graphs themselves then reflect the symmetries of the underlying data, similarly to the lifted graphical models. Inspired by lifting, we introduce a simple and efficient technique to detect the symmetries and compress the neural models without loss of any information. We demonstrate through experiments that such compression can lead to significant speedups of structured convolutional models, such as various Graph Neural Networks, across various tasks, such as molecule classification and knowledge-base completion.

Stacked Structure Learning for Lifted Relational Neural Networks

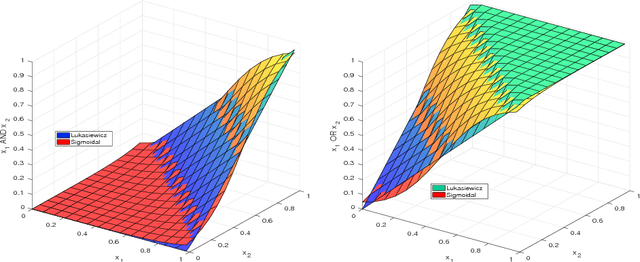
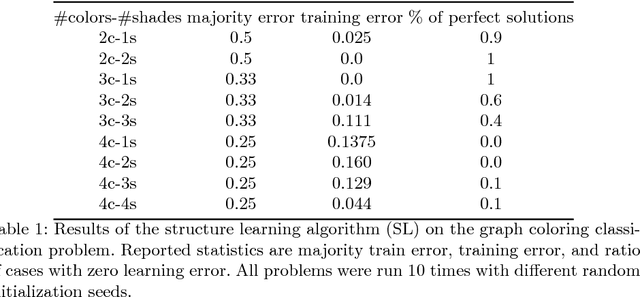
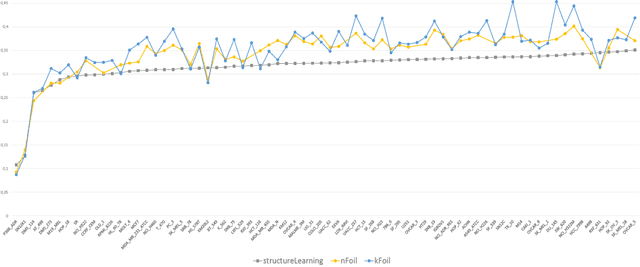
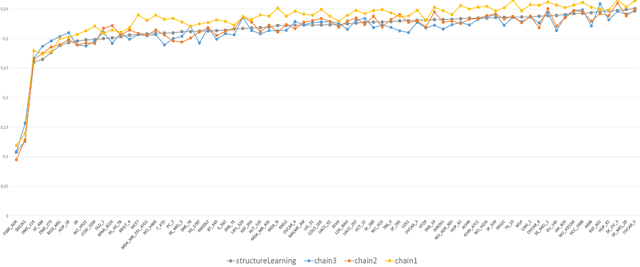
Lifted Relational Neural Networks (LRNNs) describe relational domains using weighted first-order rules which act as templates for constructing feed-forward neural networks. While previous work has shown that using LRNNs can lead to state-of-the-art results in various ILP tasks, these results depended on hand-crafted rules. In this paper, we extend the framework of LRNNs with structure learning, thus enabling a fully automated learning process. Similarly to many ILP methods, our structure learning algorithm proceeds in an iterative fashion by top-down searching through the hypothesis space of all possible Horn clauses, considering the predicates that occur in the training examples as well as invented soft concepts entailed by the best weighted rules found so far. In the experiments, we demonstrate the ability to automatically induce useful hierarchical soft concepts leading to deep LRNNs with a competitive predictive power.

Lifted Relational Neural Networks

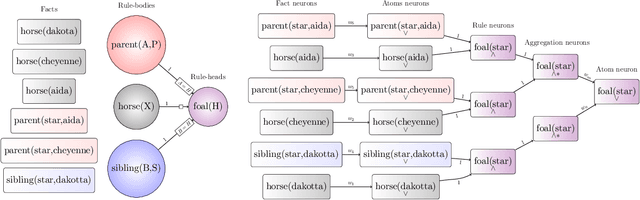
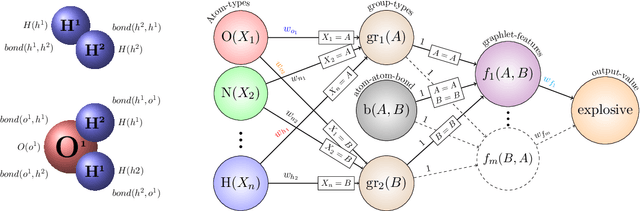
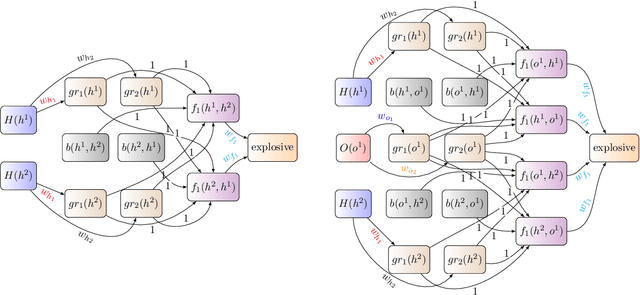
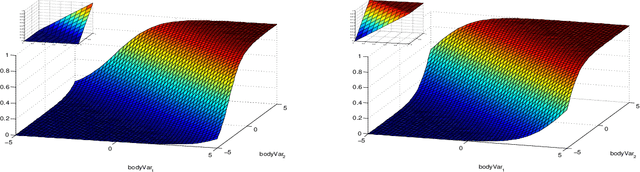
We propose a method combining relational-logic representations with neural network learning. A general lifted architecture, possibly reflecting some background domain knowledge, is described through relational rules which may be handcrafted or learned. The relational rule-set serves as a template for unfolding possibly deep neural networks whose structures also reflect the structures of given training or testing relational examples. Different networks corresponding to different examples share their weights, which co-evolve during training by stochastic gradient descent algorithm. The framework allows for hierarchical relational modeling constructs and learning of latent relational concepts through shared hidden layers weights corresponding to the rules. Discovery of notable relational concepts and experiments on 78 relational learning benchmarks demonstrate favorable performance of the method.