Geometry in Style: 3D Stylization via Surface Normal Deformation

We present Geometry in Style, a new method for identity-preserving mesh stylization. Existing techniques either adhere to the original shape through overly restrictive deformations such as bump maps or significantly modify the input shape using expressive deformations that may introduce artifacts or alter the identity of the source shape. In contrast, we represent a deformation of a triangle mesh as a target normal vector for each vertex neighborhood. The deformations we recover from target normals are expressive enough to enable detailed stylizations yet restrictive enough to preserve the shape's identity. We achieve such deformations using our novel differentiable As-Rigid-As-Possible (dARAP) layer, a neural-network-ready adaptation of the classical ARAP algorithm which we use to solve for per-vertex rotations and deformed vertices. As a differentiable layer, dARAP is paired with a visual loss from a text-to-image model to drive deformations toward style prompts, altogether giving us Geometry in Style. Our project page is at https://threedle.github.io/geometry-in-style.

Robust Biharmonic Skinning Using Geometric Fields

Skinning is a popular way to rig and deform characters for animation, to compute reduced-order simulations, and to define features for geometry processing. Methods built on skinning rely on weight functions that distribute the influence of each degree of freedom across the mesh. Automatic skinning methods generate these weight functions with minimal user input, usually by solving a variational problem on a mesh whose boundary is the skinned surface. This formulation necessitates tetrahedralizing the volume inside the surface, which brings with it meshing artifacts, the possibility of tetrahedralization failure, and the impossibility of generating weights for surfaces that are not closed. We introduce a mesh-free and robust automatic skinning method that generates high-quality skinning weights comparable to the current state of the art without volumetric meshes. Our method reliably works even on open surfaces and triangle soups where current methods fail. We achieve this through the use of a Lagrangian representation for skinning weights, which circumvents the need for finite elements while optimizing the biharmonic energy.

Variational Barycentric Coordinates

We propose a variational technique to optimize for generalized barycentric coordinates that offers additional control compared to existing models. Prior work represents barycentric coordinates using meshes or closed-form formulae, in practice limiting the choice of objective function. In contrast, we directly parameterize the continuous function that maps any coordinate in a polytope's interior to its barycentric coordinates using a neural field. This formulation is enabled by our theoretical characterization of barycentric coordinates, which allows us to construct neural fields that parameterize the entire function class of valid coordinates. We demonstrate the flexibility of our model using a variety of objective functions, including multiple smoothness and deformation-aware energies; as a side contribution, we also present mathematically-justified means of measuring and minimizing objectives like total variation on discontinuous neural fields. We offer a practical acceleration strategy, present a thorough validation of our algorithm, and demonstrate several applications.

Symmetric Volume Maps

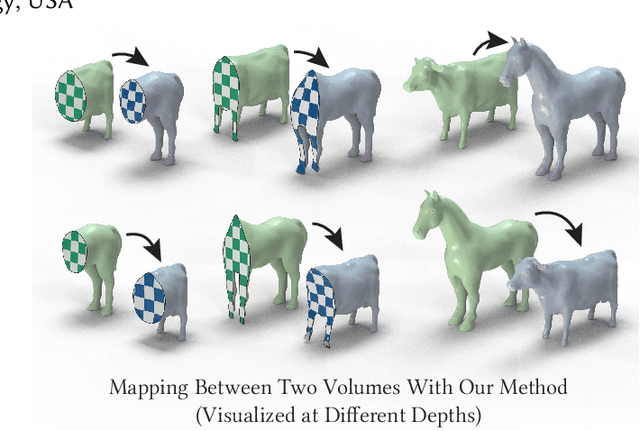
Although shape correspondence is a central problem in geometry processing, most methods for this task apply only to two-dimensional surfaces. The neglected task of volumetric correspondence--a natural extension relevant to shapes extracted from simulation, medical imaging, volume rendering, and even improving surface maps of boundary representations--presents unique challenges that do not appear in the two-dimensional case. In this work, we propose a method for mapping between volumes represented as tetrahedral meshes. Our formulation minimizes a distortion energy designed to extract maps symmetrically, i.e., without dependence on the ordering of the source and target domains. We accompany our method with theoretical discussion describing the consequences of this symmetry assumption, leading us to select a symmetrized ARAP energy that favors isometric correspondences. Our final formulation optimizes for near-isometry while matching the boundary. We demonstrate our method on a diverse geometric dataset, producing low-distortion matchings that align to the boundary.