Robust Biharmonic Skinning Using Geometric Fields

Skinning is a popular way to rig and deform characters for animation, to compute reduced-order simulations, and to define features for geometry processing. Methods built on skinning rely on weight functions that distribute the influence of each degree of freedom across the mesh. Automatic skinning methods generate these weight functions with minimal user input, usually by solving a variational problem on a mesh whose boundary is the skinned surface. This formulation necessitates tetrahedralizing the volume inside the surface, which brings with it meshing artifacts, the possibility of tetrahedralization failure, and the impossibility of generating weights for surfaces that are not closed. We introduce a mesh-free and robust automatic skinning method that generates high-quality skinning weights comparable to the current state of the art without volumetric meshes. Our method reliably works even on open surfaces and triangle soups where current methods fail. We achieve this through the use of a Lagrangian representation for skinning weights, which circumvents the need for finite elements while optimizing the biharmonic energy.

Variational Barycentric Coordinates

We propose a variational technique to optimize for generalized barycentric coordinates that offers additional control compared to existing models. Prior work represents barycentric coordinates using meshes or closed-form formulae, in practice limiting the choice of objective function. In contrast, we directly parameterize the continuous function that maps any coordinate in a polytope's interior to its barycentric coordinates using a neural field. This formulation is enabled by our theoretical characterization of barycentric coordinates, which allows us to construct neural fields that parameterize the entire function class of valid coordinates. We demonstrate the flexibility of our model using a variety of objective functions, including multiple smoothness and deformation-aware energies; as a side contribution, we also present mathematically-justified means of measuring and minimizing objectives like total variation on discontinuous neural fields. We offer a practical acceleration strategy, present a thorough validation of our algorithm, and demonstrate several applications.

Path Guiding Using Spatio-Directional Mixture Models

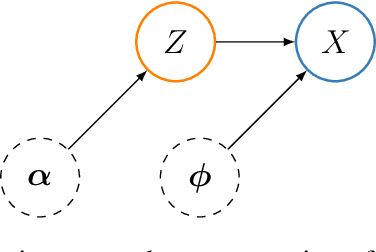
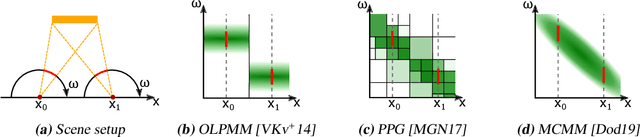
We propose a learning-based method for light-path construction in path tracing algorithms, which iteratively optimizes and samples from what we refer to as spatio-directional Gaussian mixture models (SDMMs). In particular, we approximate incident radiance as an online-trained $5$D mixture that is accelerated by a $k$D-tree. Using the same framework, we approximate BSDFs as pre-trained $n$D mixtures, where $n$ is the number of BSDF parameters. Such an approach addresses two major challenges in path-guiding models. First, the $5$D radiance representation naturally captures correlation between the spatial and directional dimensions. Such correlations are present in e.g.\ parallax and caustics. Second, by using a tangent-space parameterization of Gaussians, our spatio-directional mixtures can perform approximate product sampling with arbitrarily oriented BSDFs. Existing models are only able to do this by either foregoing anisotropy of the mixture components or by representing the radiance field in local (normal aligned) coordinates, which both make the radiance field more difficult to learn. An additional benefit of the tangent-space parameterization is that each individual Gaussian is mapped to the solid sphere with low distortion near its center of mass. Our method performs especially well on scenes with small, localized luminaires that induce high spatio-directional correlation in the incident radiance.