Incorporating Coupling Knowledge into Echo State Networks for Learning Spatiotemporally Chaotic Dynamics

Machine learning methods have shown promise in learning chaotic dynamical systems, enabling model-free short-term prediction and attractor reconstruction. However, when applied to large-scale, spatiotemporally chaotic systems, purely data-driven machine learning methods often suffer from inefficiencies, as they require a large learning model size and a massive amount of training data to achieve acceptable performance. To address this challenge, we incorporate the spatial coupling structure of the target system as an inductive bias in the network design. Specifically, we introduce physics-guided clustered echo state networks, leveraging the efficiency of the echo state networks as a base model. Experimental results on benchmark chaotic systems demonstrate that our physics-informed method outperforms existing echo state network models in learning the target chaotic systems. Additionally, our models exhibit robustness to noise in training data and remain effective even when prior coupling knowledge is imperfect. This approach has the potential to enhance other machine learning methods.

Exploiting Chaotic Dynamics as Deep Neural Networks

Chaos presents complex dynamics arising from nonlinearity and a sensitivity to initial states. These characteristics suggest a depth of expressivity that underscores their potential for advanced computational applications. However, strategies to effectively exploit chaotic dynamics for information processing have largely remained elusive. In this study, we reveal that the essence of chaos can be found in various state-of-the-art deep neural networks. Drawing inspiration from this revelation, we propose a novel method that directly leverages chaotic dynamics for deep learning architectures. Our approach is systematically evaluated across distinct chaotic systems. In all instances, our framework presents superior results to conventional deep neural networks in terms of accuracy, convergence speed, and efficiency. Furthermore, we found an active role of transient chaos formation in our scheme. Collectively, this study offers a new path for the integration of chaos, which has long been overlooked in information processing, and provides insights into the prospective fusion of chaotic dynamics within the domains of machine learning and neuromorphic computation.

Virtual reservoir acceleration for CPU and GPU: Case study for coupled spin-torque oscillator reservoir

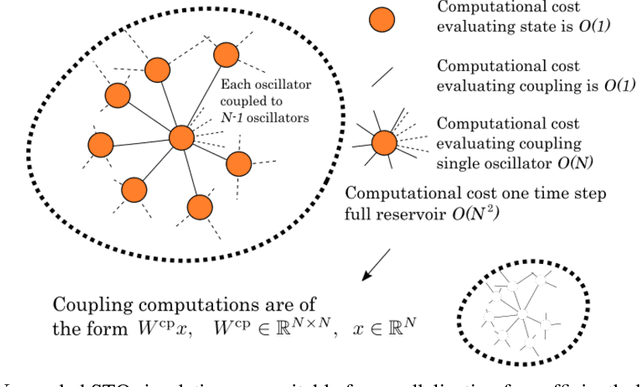
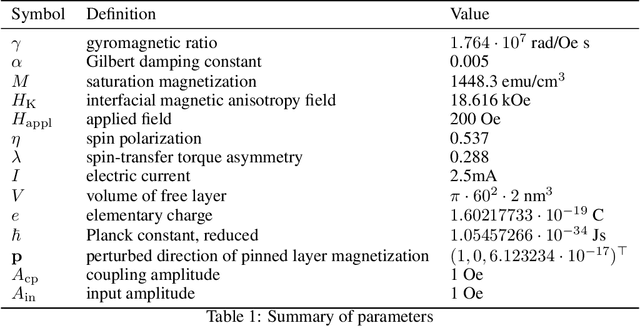
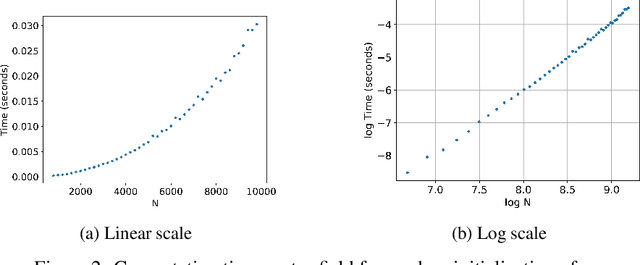
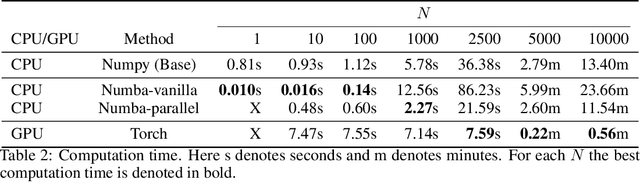
We provide high-speed implementations for simulating reservoirs described by $N$-coupled spin-torque oscillators. Here $N$ also corresponds to the number of reservoir nodes. We benchmark a variety of implementations based on CPU and GPU. Our new methods are at least 2.6 times quicker than the baseline for $N$ in range $1$ to $10^4$. More specifically, over all implementations the best factor is 78.9 for $N=1$ which decreases to 2.6 for $N=10^3$ and finally increases to 23.8 for $N=10^4$. GPU outperforms CPU significantly at $N=2500$. Our results show that GPU implementations should be tested for reservoir simulations. The implementations considered here can be used for any reservoir with evolution that can be approximated using an explicit method.

Embedding bifurcations into pneumatic artificial muscle

Harnessing complex body dynamics has been a long-standing challenge in robotics. Soft body dynamics is a typical example of high complexity in interacting with the environment. An increasing number of studies have reported that these dynamics can be used as a computational resource. This includes the McKibben pneumatic artificial muscle, which is a typical soft actuator. This study demonstrated that various dynamics, including periodic and chaotic dynamics, could be embedded into the pneumatic artificial muscle, with the entire bifurcation structure using the framework of physical reservoir computing. These results suggest that dynamics that are not presented in training data could be embedded by using this capability of bifurcation embeddment. This implies that it is possible to embed various qualitatively different patterns into pneumatic artificial muscle by learning specific patterns, without the need to design and learn all patterns required for the purpose. Thus, this study sheds new light on a novel pathway to simplify the robotic devices and training of the control by reducing the external pattern generators and the amount and types of training data for the control.