Harnessing omnipresent oscillator networks as computational resource

Nature is pervaded with oscillatory behavior. In networks of coupled oscillators patterns can arise when the system synchronizes to an external input. Hence, these networks provide processing and memory of input. We present a universal framework for harnessing oscillator networks as computational resource. This reservoir computing framework is introduced by the ubiquitous model for phase-locking, the Kuramoto model. We force the Kuramoto model by a nonlinear target-system, then after substituting the target-system with a trained feedback-loop it emulates the target-system. Our results are two-fold. Firstly, the trained network inherits performance properties of the Kuramoto model, where all-to-all coupling is performed in linear time with respect to the number of nodes and parameters for synchronization are abundant. Secondly, the learning capabilities of the oscillator network can be explained using Kuramoto model's order parameter. This work provides the foundation for utilizing nature's oscillator networks as a new class of information processing systems.

Virtual reservoir acceleration for CPU and GPU: Case study for coupled spin-torque oscillator reservoir

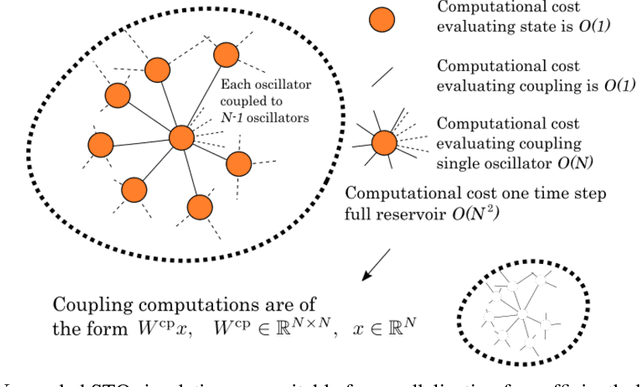
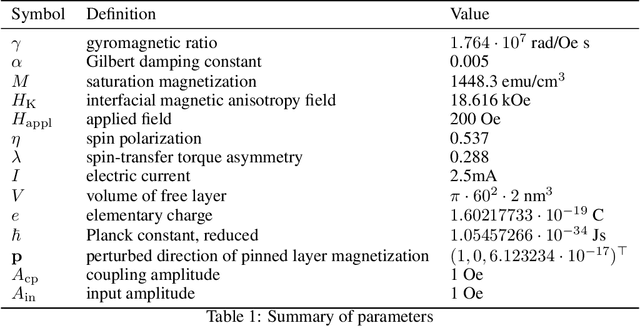
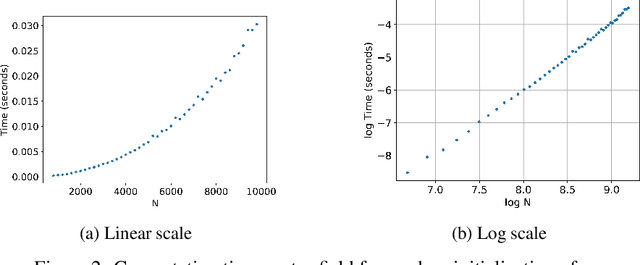
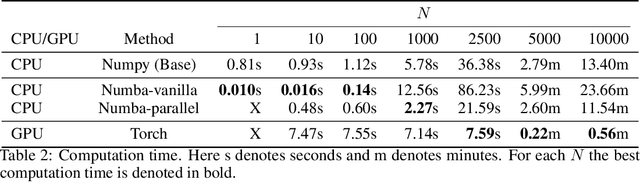
We provide high-speed implementations for simulating reservoirs described by $N$-coupled spin-torque oscillators. Here $N$ also corresponds to the number of reservoir nodes. We benchmark a variety of implementations based on CPU and GPU. Our new methods are at least 2.6 times quicker than the baseline for $N$ in range $1$ to $10^4$. More specifically, over all implementations the best factor is 78.9 for $N=1$ which decreases to 2.6 for $N=10^3$ and finally increases to 23.8 for $N=10^4$. GPU outperforms CPU significantly at $N=2500$. Our results show that GPU implementations should be tested for reservoir simulations. The implementations considered here can be used for any reservoir with evolution that can be approximated using an explicit method.