Latency-Distortion Tradeoffs in Communicating Classification Results over Noisy Channels

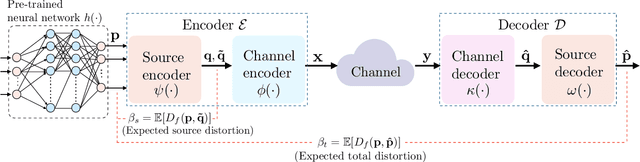
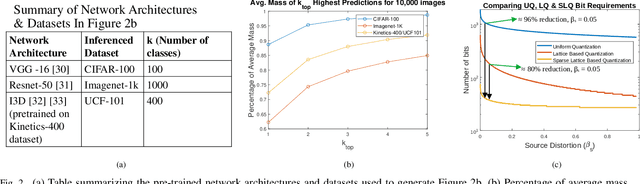
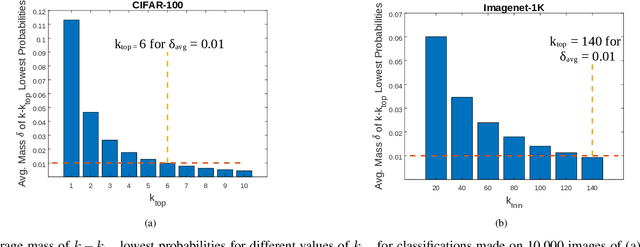
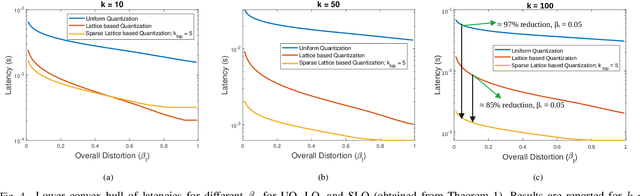
In this work, the problem of communicating decisions of a classifier over a noisy channel is considered. With machine learning based models being used in variety of time-sensitive applications, transmission of these decisions in a reliable and timely manner is of significant importance. To this end, we study the scenario where a probability vector (representing the decisions of a classifier) at the transmitter, needs to be transmitted over a noisy channel. Assuming that the distortion between the original probability vector and the reconstructed one at the receiver is measured via f-divergence, we study the trade-off between transmission latency and the distortion. We completely analyze this trade-off using uniform, lattice, and sparse lattice-based quantization techniques to encode the probability vector by first characterizing bit budgets for each technique given a requirement on the allowed source distortion. These bounds are then combined with results from finite-blocklength literature to provide a framework for analyzing the effects of both quantization distortion and distortion due to decoding error probability (i.e., channel effects) on the incurred transmission latency. Our results show that there is an interesting interplay between source distortion (i.e., distortion for the probability vector measured via f-divergence) and the subsequent channel encoding/decoding parameters; and indicate that a joint design of these parameters is crucial to navigate the latency-distortion tradeoff. We study the impact of changing different parameters (e.g. number of classes, SNR, source distortion) on the latency-distortion tradeoff and perform experiments on AWGN and fading channels. Our results indicate that sparse lattice-based quantization is the most effective at minimizing latency across various regimes and for sparse, high-dimensional probability vectors (i.e., high number of classes).

Adversarial Filters for Secure Modulation Classification

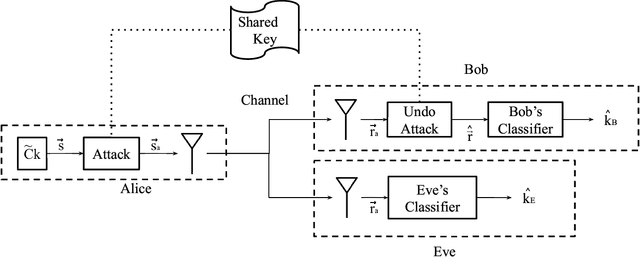
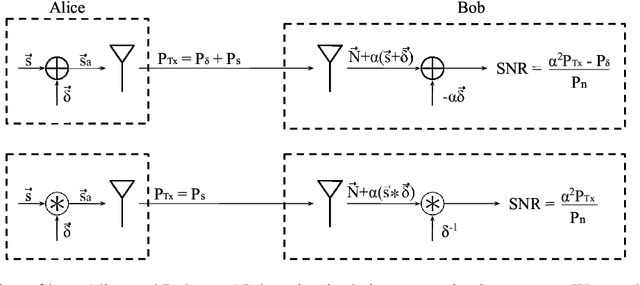
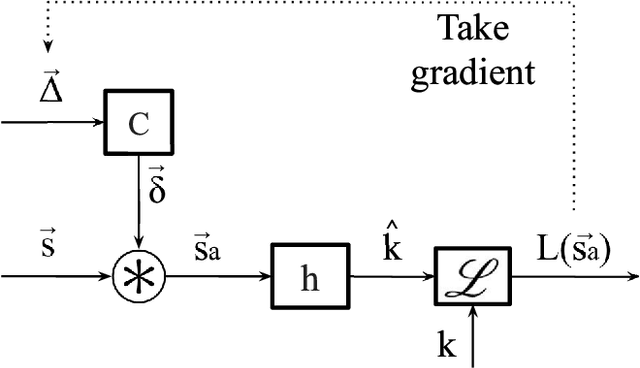
Modulation Classification (MC) refers to the problem of classifying the modulation class of a wireless signal. In the wireless communications pipeline, MC is the first operation performed on the received signal and is critical for reliable decoding. This paper considers the problem of secure modulation classification, where a transmitter (Alice) wants to maximize MC accuracy at a legitimate receiver (Bob) while minimizing MC accuracy at an eavesdropper (Eve). The contribution of this work is to design novel adversarial learning techniques for secure MC. In particular, we present adversarial filtering based algorithms for secure MC, in which Alice uses a carefully designed adversarial filter to mask the transmitted signal, that can maximize MC accuracy at Bob while minimizing MC accuracy at Eve. We present two filtering based algorithms, namely gradient ascent filter (GAF), and a fast gradient filter method (FGFM), with varying levels of complexity. Our proposed adversarial filtering based approaches significantly outperform additive adversarial perturbations (used in the traditional ML community and other prior works on secure MC) and also have several other desirable properties. In particular, GAF and FGFM algorithms are a) computational efficient (allow fast decoding at Bob), b) power-efficient (do not require excessive transmit power at Alice); and c) SNR efficient (i.e., perform well even at low SNR values at Bob).