Fine-Grained Uncertainty Quantification via Collisions

We propose a new approach for fine-grained uncertainty quantification (UQ) using a collision matrix. For a classification problem involving $K$ classes, the $K\times K$ collision matrix $S$ measures the inherent (aleatoric) difficulty in distinguishing between each pair of classes. In contrast to existing UQ methods, the collision matrix gives a much more detailed picture of the difficulty of classification. We discuss several possible downstream applications of the collision matrix, establish its fundamental mathematical properties, as well as show its relationship with existing UQ methods, including the Bayes error rate. We also address the new problem of estimating the collision matrix using one-hot labeled data. We propose a series of innovative techniques to estimate $S$. First, we learn a contrastive binary classifier which takes two inputs and determines if they belong to the same class. We then show that this contrastive classifier (which is PAC learnable) can be used to reliably estimate the Gramian matrix of $S$, defined as $G=S^TS$. Finally, we show that under very mild assumptions, $G$ can be used to uniquely recover $S$, a new result on stochastic matrices which could be of independent interest. Experimental results are also presented to validate our methods on several datasets.

Trustworthy Actionable Perturbations

Counterfactuals, or modified inputs that lead to a different outcome, are an important tool for understanding the logic used by machine learning classifiers and how to change an undesirable classification. Even if a counterfactual changes a classifier's decision, however, it may not affect the true underlying class probabilities, i.e. the counterfactual may act like an adversarial attack and ``fool'' the classifier. We propose a new framework for creating modified inputs that change the true underlying probabilities in a beneficial way which we call Trustworthy Actionable Perturbations (TAP). This includes a novel verification procedure to ensure that TAP change the true class probabilities instead of acting adversarially. Our framework also includes new cost, reward, and goal definitions that are better suited to effectuating change in the real world. We present PAC-learnability results for our verification procedure and theoretically analyze our new method for measuring reward. We also develop a methodology for creating TAP and compare our results to those achieved by previous counterfactual methods.

Latency-Distortion Tradeoffs in Communicating Classification Results over Noisy Channels

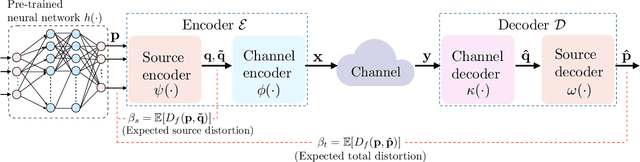
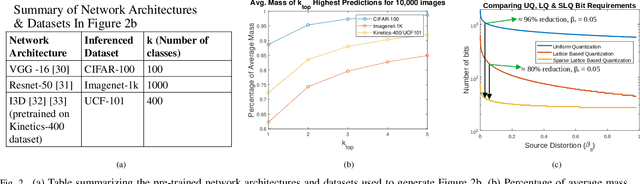
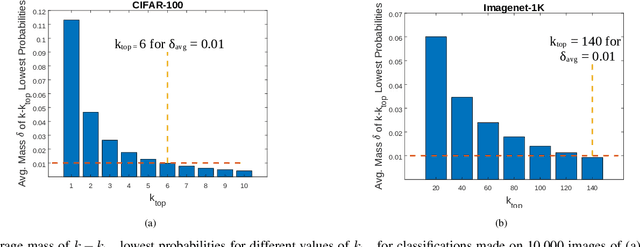
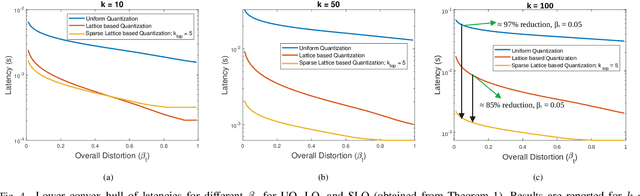
In this work, the problem of communicating decisions of a classifier over a noisy channel is considered. With machine learning based models being used in variety of time-sensitive applications, transmission of these decisions in a reliable and timely manner is of significant importance. To this end, we study the scenario where a probability vector (representing the decisions of a classifier) at the transmitter, needs to be transmitted over a noisy channel. Assuming that the distortion between the original probability vector and the reconstructed one at the receiver is measured via f-divergence, we study the trade-off between transmission latency and the distortion. We completely analyze this trade-off using uniform, lattice, and sparse lattice-based quantization techniques to encode the probability vector by first characterizing bit budgets for each technique given a requirement on the allowed source distortion. These bounds are then combined with results from finite-blocklength literature to provide a framework for analyzing the effects of both quantization distortion and distortion due to decoding error probability (i.e., channel effects) on the incurred transmission latency. Our results show that there is an interesting interplay between source distortion (i.e., distortion for the probability vector measured via f-divergence) and the subsequent channel encoding/decoding parameters; and indicate that a joint design of these parameters is crucial to navigate the latency-distortion tradeoff. We study the impact of changing different parameters (e.g. number of classes, SNR, source distortion) on the latency-distortion tradeoff and perform experiments on AWGN and fading channels. Our results indicate that sparse lattice-based quantization is the most effective at minimizing latency across various regimes and for sparse, high-dimensional probability vectors (i.e., high number of classes).

Generalization Bounds for Neural Belief Propagation Decoders

Machine learning based approaches are being increasingly used for designing decoders for next generation communication systems. One widely used framework is neural belief propagation (NBP), which unfolds the belief propagation (BP) iterations into a deep neural network and the parameters are trained in a data-driven manner. NBP decoders have been shown to improve upon classical decoding algorithms. In this paper, we investigate the generalization capabilities of NBP decoders. Specifically, the generalization gap of a decoder is the difference between empirical and expected bit-error-rate(s). We present new theoretical results which bound this gap and show the dependence on the decoder complexity, in terms of code parameters (blocklength, message length, variable/check node degrees), decoding iterations, and the training dataset size. Results are presented for both regular and irregular parity-check matrices. To the best of our knowledge, this is the first set of theoretical results on generalization performance of neural network based decoders. We present experimental results to show the dependence of generalization gap on the training dataset size, and decoding iterations for different codes.

Unsupervised Change Detection using DRE-CUSUM

This paper presents DRE-CUSUM, an unsupervised density-ratio estimation (DRE) based approach to determine statistical changes in time-series data when no knowledge of the pre-and post-change distributions are available. The core idea behind the proposed approach is to split the time-series at an arbitrary point and estimate the ratio of densities of distribution (using a parametric model such as a neural network) before and after the split point. The DRE-CUSUM change detection statistic is then derived from the cumulative sum (CUSUM) of the logarithm of the estimated density ratio. We present a theoretical justification as well as accuracy guarantees which show that the proposed statistic can reliably detect statistical changes, irrespective of the split point. While there have been prior works on using density ratio based methods for change detection, to the best of our knowledge, this is the first unsupervised change detection approach with a theoretical justification and accuracy guarantees. The simplicity of the proposed framework makes it readily applicable in various practical settings (including high-dimensional time-series data); we also discuss generalizations for online change detection. We experimentally show the superiority of DRE-CUSUM using both synthetic and real-world datasets over existing state-of-the-art unsupervised algorithms (such as Bayesian online change detection, its variants as well as several other heuristic methods).