Latency-Distortion Tradeoffs in Communicating Classification Results over Noisy Channels

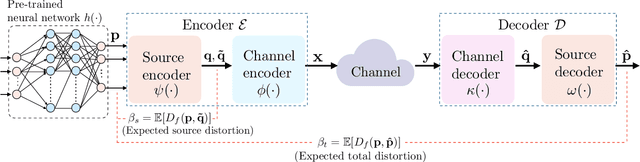
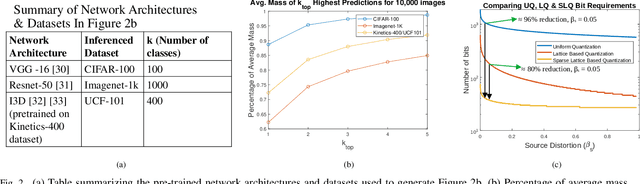
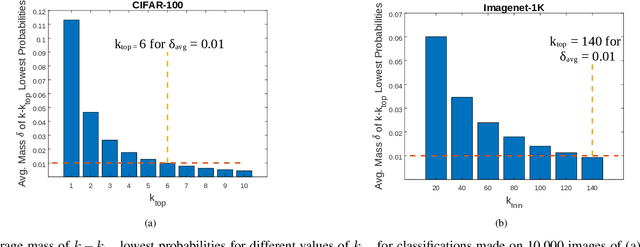
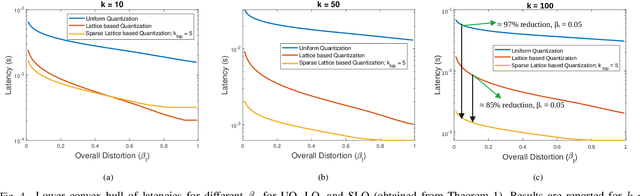
In this work, the problem of communicating decisions of a classifier over a noisy channel is considered. With machine learning based models being used in variety of time-sensitive applications, transmission of these decisions in a reliable and timely manner is of significant importance. To this end, we study the scenario where a probability vector (representing the decisions of a classifier) at the transmitter, needs to be transmitted over a noisy channel. Assuming that the distortion between the original probability vector and the reconstructed one at the receiver is measured via f-divergence, we study the trade-off between transmission latency and the distortion. We completely analyze this trade-off using uniform, lattice, and sparse lattice-based quantization techniques to encode the probability vector by first characterizing bit budgets for each technique given a requirement on the allowed source distortion. These bounds are then combined with results from finite-blocklength literature to provide a framework for analyzing the effects of both quantization distortion and distortion due to decoding error probability (i.e., channel effects) on the incurred transmission latency. Our results show that there is an interesting interplay between source distortion (i.e., distortion for the probability vector measured via f-divergence) and the subsequent channel encoding/decoding parameters; and indicate that a joint design of these parameters is crucial to navigate the latency-distortion tradeoff. We study the impact of changing different parameters (e.g. number of classes, SNR, source distortion) on the latency-distortion tradeoff and perform experiments on AWGN and fading channels. Our results indicate that sparse lattice-based quantization is the most effective at minimizing latency across various regimes and for sparse, high-dimensional probability vectors (i.e., high number of classes).