Chaotic Map based Compression Approach to Classification

Modern machine learning approaches often prioritize performance at the cost of increased complexity, computational demands, and reduced interpretability. This paper introduces a novel framework that challenges this trend by reinterpreting learning from an information-theoretic perspective, viewing it as a search for encoding schemes that capture intrinsic data structures through compact representations. Rather than following the conventional approach of fitting data to complex models, we propose a fundamentally different method that maps data to intervals of initial conditions in a dynamical system. Our GLS (Generalized L\"uroth Series) coding compression classifier employs skew tent maps - a class of chaotic maps - both for encoding data into initial conditions and for subsequent recovery. The effectiveness of this simple framework is noteworthy, with performance closely approaching that of well-established machine learning methods. On the breast cancer dataset, our approach achieves 92.98\% accuracy, comparable to Naive Bayes at 94.74\%. While these results do not exceed state-of-the-art performance, the significance of our contribution lies not in outperforming existing methods but in demonstrating that a fundamentally simpler, more interpretable approach can achieve competitive results.

Integrating Causality with Neurochaos Learning: Proposed Approach and Research Agenda

Deep learning implemented via neural networks, has revolutionized machine learning by providing methods for complex tasks such as object detection/classification and prediction. However, architectures based on deep neural networks have started to yield diminishing returns, primarily due to their statistical nature and inability to capture causal structure in the training data. Another issue with deep learning is its high energy consumption, which is not that desirable from a sustainability perspective. Therefore, alternative approaches are being considered to address these issues, both of which are inspired by the functioning of the human brain. One approach is causal learning, which takes into account causality among the items in the dataset on which the neural network is trained. It is expected that this will help minimize the spurious correlations that are prevalent in the learned representations of deep neural networks. The other approach is Neurochaos Learning, a recent development, which draws its inspiration from the nonlinear chaotic firing intrinsic to neurons in biological neural networks (brain/central nervous system). Both approaches have shown improved results over just deep learning alone. To that end, in this position paper, we investigate how causal and neurochaos learning approaches can be integrated together to produce better results, especially in domains that contain linked data. We propose an approach for this integration to enhance classification, prediction and reinforcement learning. We also propose a set of research questions that need to be investigated in order to make this integration a reality.

Causal Discovery and Classification Using Lempel-Ziv Complexity

Inferring causal relationships in the decision-making processes of machine learning algorithms is a crucial step toward achieving explainable Artificial Intelligence (AI). In this research, we introduce a novel causality measure and a distance metric derived from Lempel-Ziv (LZ) complexity. We explore how the proposed causality measure can be used in decision trees by enabling splits based on features that most strongly \textit{cause} the outcome. We further evaluate the effectiveness of the causality-based decision tree and the distance-based decision tree in comparison to a traditional decision tree using Gini impurity. While the proposed methods demonstrate comparable classification performance overall, the causality-based decision tree significantly outperforms both the distance-based decision tree and the Gini-based decision tree on datasets generated from causal models. This result indicates that the proposed approach can capture insights beyond those of classical decision trees, especially in causally structured data. Based on the features used in the LZ causal measure based decision tree, we introduce a causal strength for each features in the dataset so as to infer the predominant causal variables for the occurrence of the outcome.

Random Heterogeneous Neurochaos Learning Architecture for Data Classification

Inspired by the human brain's structure and function, Artificial Neural Networks (ANN) were developed for data classification. However, existing Neural Networks, including Deep Neural Networks, do not mimic the brain's rich structure. They lack key features such as randomness and neuron heterogeneity, which are inherently chaotic in their firing behavior. Neurochaos Learning (NL), a chaos-based neural network, recently employed one-dimensional chaotic maps like Generalized L\"uroth Series (GLS) and Logistic map as neurons. For the first time, we propose a random heterogeneous extension of NL, where various chaotic neurons are randomly placed in the input layer, mimicking the randomness and heterogeneous nature of human brain networks. We evaluated the performance of the newly proposed Random Heterogeneous Neurochaos Learning (RHNL) architectures combined with traditional Machine Learning (ML) methods. On public datasets, RHNL outperformed both homogeneous NL and fixed heterogeneous NL architectures in nearly all classification tasks. RHNL achieved high F1 scores on the Wine dataset (1.0), Bank Note Authentication dataset (0.99), Breast Cancer Wisconsin dataset (0.99), and Free Spoken Digit Dataset (FSDD) (0.98). These RHNL results are among the best in the literature for these datasets. We investigated RHNL performance on image datasets, where it outperformed stand-alone ML classifiers. In low training sample regimes, RHNL was the best among stand-alone ML. Our architecture bridges the gap between existing ANN architectures and the human brain's chaotic, random, and heterogeneous properties. We foresee the development of several novel learning algorithms centered around Random Heterogeneous Neurochaos Learning in the coming days.

Evaluating the Determinants of Mode Choice Using Statistical and Machine Learning Techniques in the Indian Megacity of Bengaluru

The decision making involved behind the mode choice is critical for transportation planning. While statistical learning techniques like discrete choice models have been used traditionally, machine learning (ML) models have gained traction recently among the transportation planners due to their higher predictive performance. However, the black box nature of ML models pose significant interpretability challenges, limiting their practical application in decision and policy making. This study utilised a dataset of $1350$ households belonging to low and low-middle income bracket in the city of Bengaluru to investigate mode choice decision making behaviour using Multinomial logit model and ML classifiers like decision trees, random forests, extreme gradient boosting and support vector machines. In terms of accuracy, random forest model performed the best ($0.788$ on training data and $0.605$ on testing data) compared to all the other models. This research has adopted modern interpretability techniques like feature importance and individual conditional expectation plots to explain the decision making behaviour using ML models. A higher travel costs significantly reduce the predicted probability of bus usage compared to other modes (a $0.66\%$ and $0.34\%$ reduction using Random Forests and XGBoost model for $10\%$ increase in travel cost). However, reducing travel time by $10\%$ increases the preference for the metro ($0.16\%$ in Random Forests and 0.42% in XGBoost). This research augments the ongoing research on mode choice analysis using machine learning techniques, which would help in improving the understanding of the performance of these models with real-world data in terms of both accuracy and interpretability.

Compression Spectrum: Where Shannon meets Fourier

Signal processing and Information theory are two disparate fields used for characterizing signals for various scientific and engineering applications. Spectral/Fourier analysis, a technique employed in signal processing, helps estimation of power at different frequency components present in the signal. Characterizing a time-series based on its average amount of information (Shannon entropy) is useful for estimating its complexity and compressibility (eg., for communication applications). Information theory doesn't deal with spectral content while signal processing doesn't directly consider the information content or compressibility of the signal. In this work, we attempt to bring the fields of signal processing and information theory together by using a lossless data compression algorithm to estimate the amount of information or `compressibility' of time series at different scales. To this end, we employ the Effort-to-Compress (ETC) algorithm to obtain what we call as a Compression Spectrum. This new tool for signal analysis is demonstrated on synthetically generated periodic signals, a sinusoid, chaotic signals (weak and strong chaos) and uniform random noise. The Compression Spectrum is applied on heart interbeat intervals (RR) obtained from real-world normal young and elderly subjects. The compression spectrum of healthy young RR tachograms in the log-log scale shows behaviour similar to $1/f$ noise whereas the healthy old RR tachograms show a different behaviour. We envisage exciting possibilities and future applications of the Compression Spectrum.

To prune or not to prune : A chaos-causality approach to principled pruning of dense neural networks

Reducing the size of a neural network (pruning) by removing weights without impacting its performance is an important problem for resource-constrained devices. In the past, pruning was typically accomplished by ranking or penalizing weights based on criteria like magnitude and removing low-ranked weights before retraining the remaining ones. Pruning strategies may also involve removing neurons from the network in order to achieve the desired reduction in network size. We formulate pruning as an optimization problem with the objective of minimizing misclassifications by selecting specific weights. To accomplish this, we have introduced the concept of chaos in learning (Lyapunov exponents) via weight updates and exploiting causality to identify the causal weights responsible for misclassification. Such a pruned network maintains the original performance and retains feature explainability.

Permutation Decision Trees

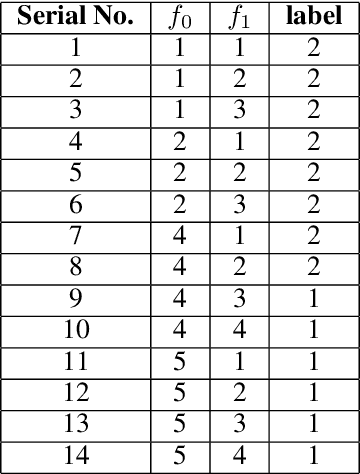
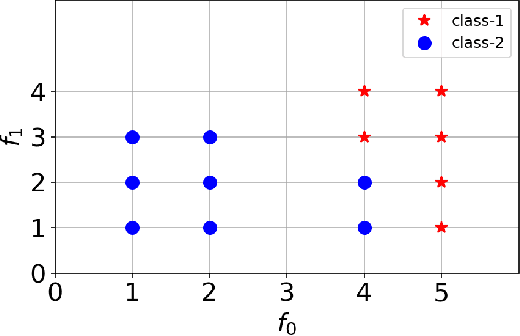
Decision Tree is a well understood Machine Learning model that is based on minimizing impurities in the internal nodes. The most common impurity measures are Shannon entropy and Gini impurity. These impurity measures are insensitive to the order of training data and hence the final tree obtained is invariant to any permutation of the data. This leads to a serious limitation in modeling data instances that have order dependencies. In this work, we propose the use of Effort-To-Compress (ETC) - a complexity measure, for the first time, as an impurity measure. Unlike Shannon entropy and Gini impurity, structural impurity based on ETC is able to capture order dependencies in the data, thus obtaining potentially different decision trees for different permutations of the same data instances (Permutation Decision Trees). We then introduce the notion of Permutation Bagging achieved using permutation decision trees without the need for random feature selection and sub-sampling. We compare the performance of the proposed permutation bagged decision trees with Random Forests. Our model does not assume that the data instances are independent and identically distributed. Potential applications include scenarios where a temporal order present in the data instances is to be respected.

Cause-Effect Preservation and Classification using Neurochaos Learning

Discovering cause-effect from observational data is an important but challenging problem in science and engineering. In this work, a recently proposed brain inspired learning algorithm namely-\emph{Neurochaos Learning} (NL) is used for the classification of cause-effect from simulated data. The data instances used are generated from coupled AR processes, coupled 1D chaotic skew tent maps, coupled 1D chaotic logistic maps and a real-world prey-predator system. The proposed method consistently outperforms a five layer Deep Neural Network architecture for coupling coefficient values ranging from $0.1$ to $0.7$. Further, we investigate the preservation of causality in the feature extracted space of NL using Granger Causality (GC) for coupled AR processes and and Compression-Complexity Causality (CCC) for coupled chaotic systems and real-world prey-predator dataset. This ability of NL to preserve causality under a chaotic transformation and successfully classify cause and effect time series (including a transfer learning scenario) is highly desirable in causal machine learning applications.

Learning Generalized Causal Structure in Time-series

The science of causality explains/determines 'cause-effect' relationship between the entities of a system by providing mathematical tools for the purpose. In spite of all the success and widespread applications of machine-learning (ML) algorithms, these algorithms are based on statistical learning alone. Currently, they are nowhere close to 'human-like' intelligence as they fail to answer and learn based on the important "Why?" questions. Hence, researchers are attempting to integrate ML with the science of causality. Among the many causal learning issues encountered by ML, one is that these algorithms are dumb to the temporal order or structure in data. In this work we develop a machine learning pipeline based on a recently proposed 'neurochaos' feature learning technique (ChaosFEX feature extractor), that helps us to learn generalized causal-structure in given time-series data.