Compression Spectrum: Where Shannon meets Fourier

Signal processing and Information theory are two disparate fields used for characterizing signals for various scientific and engineering applications. Spectral/Fourier analysis, a technique employed in signal processing, helps estimation of power at different frequency components present in the signal. Characterizing a time-series based on its average amount of information (Shannon entropy) is useful for estimating its complexity and compressibility (eg., for communication applications). Information theory doesn't deal with spectral content while signal processing doesn't directly consider the information content or compressibility of the signal. In this work, we attempt to bring the fields of signal processing and information theory together by using a lossless data compression algorithm to estimate the amount of information or `compressibility' of time series at different scales. To this end, we employ the Effort-to-Compress (ETC) algorithm to obtain what we call as a Compression Spectrum. This new tool for signal analysis is demonstrated on synthetically generated periodic signals, a sinusoid, chaotic signals (weak and strong chaos) and uniform random noise. The Compression Spectrum is applied on heart interbeat intervals (RR) obtained from real-world normal young and elderly subjects. The compression spectrum of healthy young RR tachograms in the log-log scale shows behaviour similar to $1/f$ noise whereas the healthy old RR tachograms show a different behaviour. We envisage exciting possibilities and future applications of the Compression Spectrum.

Cause-Effect Preservation and Classification using Neurochaos Learning

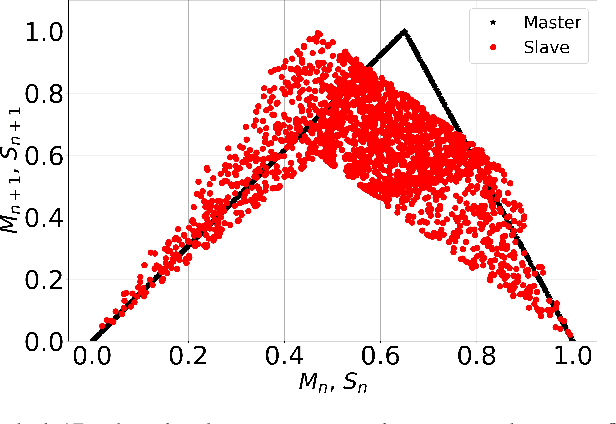
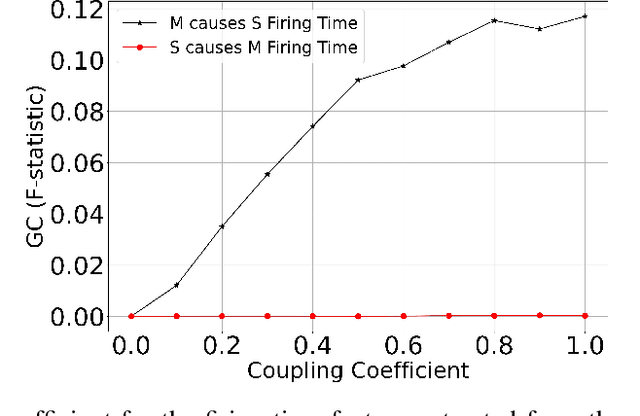
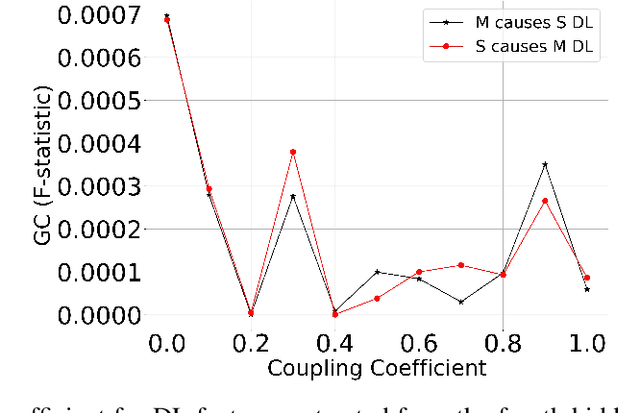
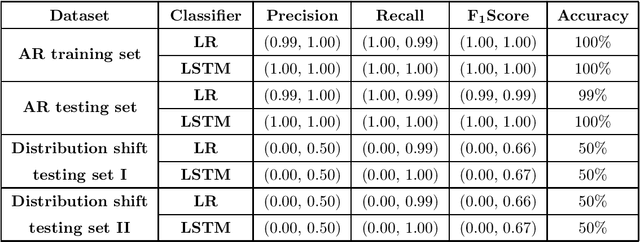
Discovering cause-effect from observational data is an important but challenging problem in science and engineering. In this work, a recently proposed brain inspired learning algorithm namely-\emph{Neurochaos Learning} (NL) is used for the classification of cause-effect from simulated data. The data instances used are generated from coupled AR processes, coupled 1D chaotic skew tent maps, coupled 1D chaotic logistic maps and a real-world prey-predator system. The proposed method consistently outperforms a five layer Deep Neural Network architecture for coupling coefficient values ranging from $0.1$ to $0.7$. Further, we investigate the preservation of causality in the feature extracted space of NL using Granger Causality (GC) for coupled AR processes and and Compression-Complexity Causality (CCC) for coupled chaotic systems and real-world prey-predator dataset. This ability of NL to preserve causality under a chaotic transformation and successfully classify cause and effect time series (including a transfer learning scenario) is highly desirable in causal machine learning applications.

Learning Generalized Causal Structure in Time-series

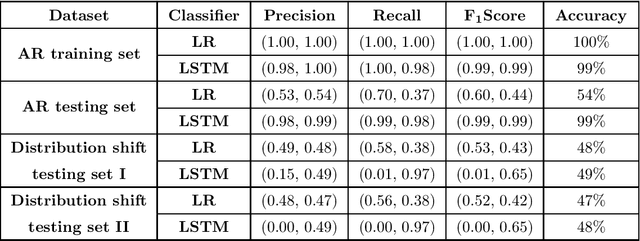
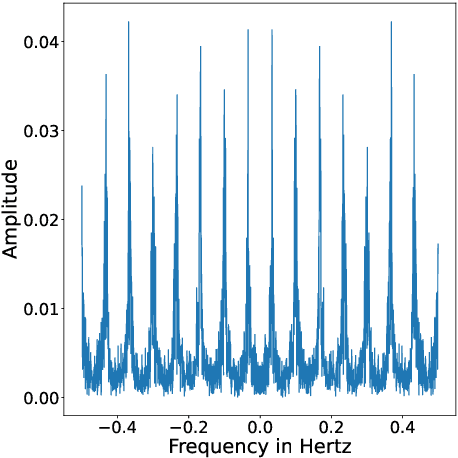
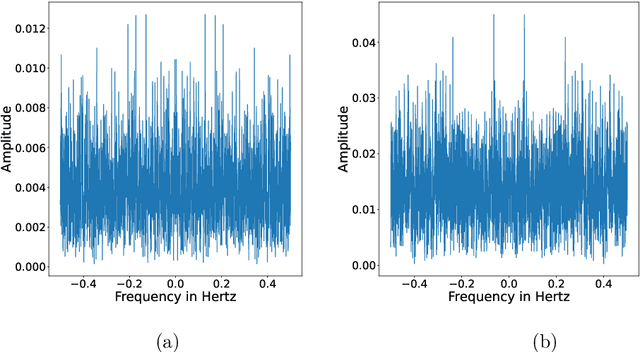
The science of causality explains/determines 'cause-effect' relationship between the entities of a system by providing mathematical tools for the purpose. In spite of all the success and widespread applications of machine-learning (ML) algorithms, these algorithms are based on statistical learning alone. Currently, they are nowhere close to 'human-like' intelligence as they fail to answer and learn based on the important "Why?" questions. Hence, researchers are attempting to integrate ML with the science of causality. Among the many causal learning issues encountered by ML, one is that these algorithms are dumb to the temporal order or structure in data. In this work we develop a machine learning pipeline based on a recently proposed 'neurochaos' feature learning technique (ChaosFEX feature extractor), that helps us to learn generalized causal-structure in given time-series data.

ChaosNet: A Chaos based Artificial Neural Network Architecture for Classification

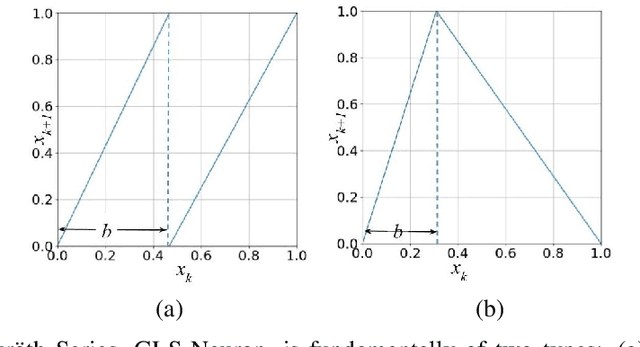
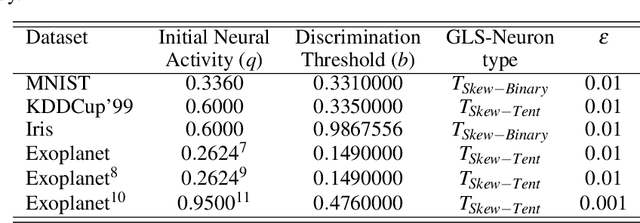
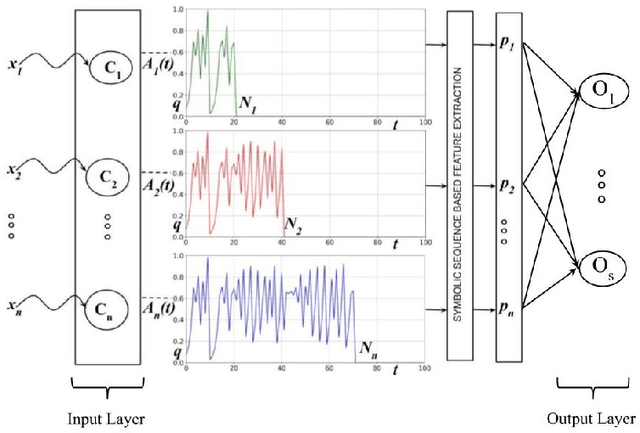
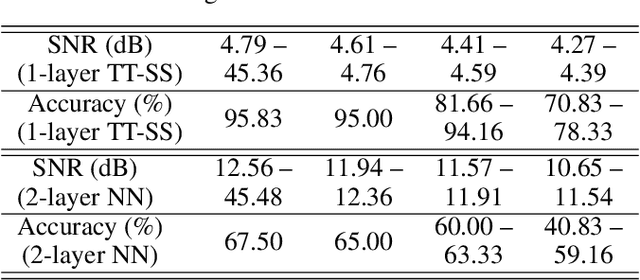
Inspired by chaotic firing of neurons in the brain, we propose ChaosNet -- a novel chaos based artificial neural network architecture for classification tasks. ChaosNet is built using layers of neurons, each of which is a 1D chaotic map known as the Generalized Luroth Series (GLS) which has been shown in earlier works to possess very useful properties for compression, cryptography and for computing XOR and other logical operations. In this work, we design a novel learning algorithm on ChaosNet that exploits the topological transitivity property of the chaotic GLS neurons. The proposed learning algorithm gives consistently good performance accuracy in a number of classification tasks on well known publicly available datasets with very limited training samples. Even with as low as 7 (or fewer) training samples/class (which accounts for less than 0.05% of the total available data), ChaosNet yields performance accuracies in the range 73.89 % - 98.33 %. We demonstrate the robustness of ChaosNet to additive parameter noise and also provide an example implementation of a 2-layer ChaosNet for enhancing classification accuracy. We envisage the development of several other novel learning algorithms on ChaosNet in the near future.