Predicting Stock Prices using Permutation Decision Trees and Strategic Trailing

In this paper, we explore the application of Permutation Decision Trees (PDT) and strategic trailing for predicting stock market movements and executing profitable trades in the Indian stock market. We focus on high-frequency data using 5-minute candlesticks for the top 50 stocks listed in the NIFTY 50 index. We implement a trading strategy that aims to buy stocks at lower prices and sell them at higher prices, capitalizing on short-term market fluctuations. Due to regulatory constraints in India, short selling is not considered in our strategy. The model incorporates various technical indicators and employs hyperparameters such as the trailing stop-loss value and support thresholds to manage risk effectively. Our results indicate that the proposed trading bot has the potential to outperform the market average and yield returns higher than the risk-free rate offered by 10-year Indian government bonds. We trained and tested data on a 60 day dataset provided by Yahoo Finance. Specifically, 12 days for testing and 48 days for training. Our bot based on permutation decision tree achieved a profit of 1.3468 % over a 12-day testing period, where as a bot based on LSTM gave a return of 0.1238 % over a 12-day testing period and a bot based on RNN gave a return of 0.3096 % over a 12-day testing period. All of the bots outperform the buy-and-hold strategy, which resulted in a loss of 2.2508 %.

Chaotic Map based Compression Approach to Classification

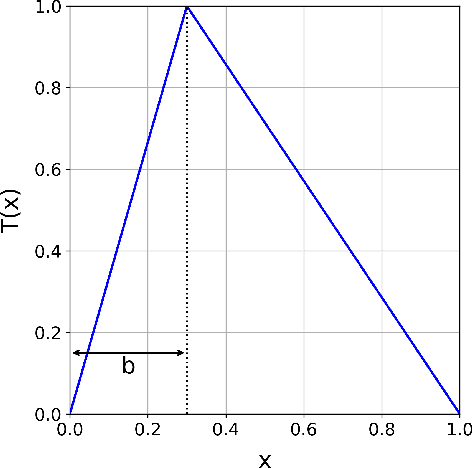
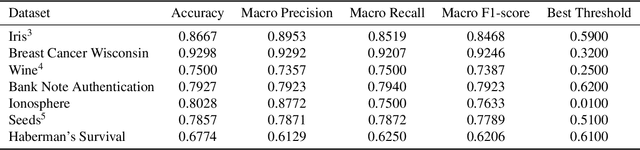
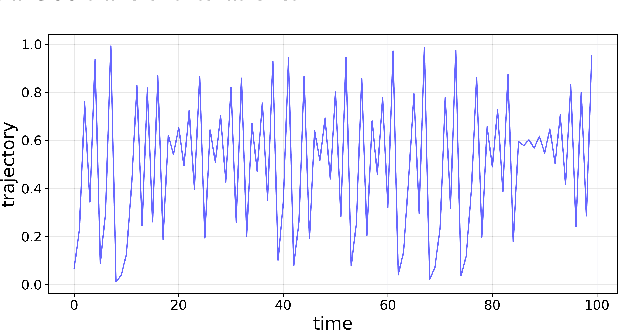
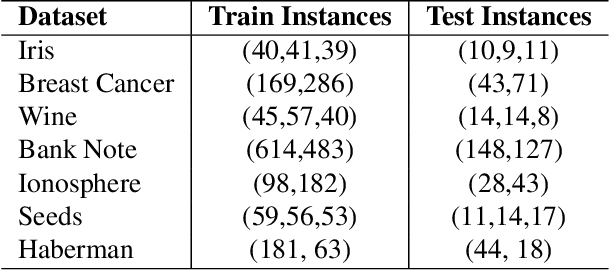
Modern machine learning approaches often prioritize performance at the cost of increased complexity, computational demands, and reduced interpretability. This paper introduces a novel framework that challenges this trend by reinterpreting learning from an information-theoretic perspective, viewing it as a search for encoding schemes that capture intrinsic data structures through compact representations. Rather than following the conventional approach of fitting data to complex models, we propose a fundamentally different method that maps data to intervals of initial conditions in a dynamical system. Our GLS (Generalized L\"uroth Series) coding compression classifier employs skew tent maps - a class of chaotic maps - both for encoding data into initial conditions and for subsequent recovery. The effectiveness of this simple framework is noteworthy, with performance closely approaching that of well-established machine learning methods. On the breast cancer dataset, our approach achieves 92.98\% accuracy, comparable to Naive Bayes at 94.74\%. While these results do not exceed state-of-the-art performance, the significance of our contribution lies not in outperforming existing methods but in demonstrating that a fundamentally simpler, more interpretable approach can achieve competitive results.

Causal Discovery and Classification Using Lempel-Ziv Complexity

Inferring causal relationships in the decision-making processes of machine learning algorithms is a crucial step toward achieving explainable Artificial Intelligence (AI). In this research, we introduce a novel causality measure and a distance metric derived from Lempel-Ziv (LZ) complexity. We explore how the proposed causality measure can be used in decision trees by enabling splits based on features that most strongly \textit{cause} the outcome. We further evaluate the effectiveness of the causality-based decision tree and the distance-based decision tree in comparison to a traditional decision tree using Gini impurity. While the proposed methods demonstrate comparable classification performance overall, the causality-based decision tree significantly outperforms both the distance-based decision tree and the Gini-based decision tree on datasets generated from causal models. This result indicates that the proposed approach can capture insights beyond those of classical decision trees, especially in causally structured data. Based on the features used in the LZ causal measure based decision tree, we introduce a causal strength for each features in the dataset so as to infer the predominant causal variables for the occurrence of the outcome.

Permutation Decision Trees

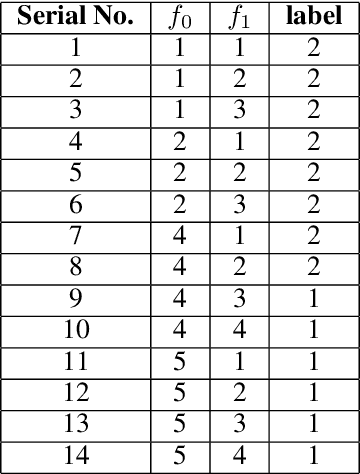
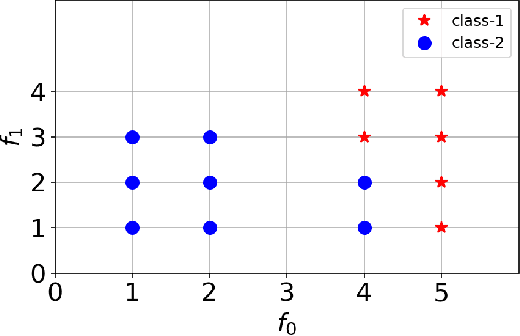
Decision Tree is a well understood Machine Learning model that is based on minimizing impurities in the internal nodes. The most common impurity measures are Shannon entropy and Gini impurity. These impurity measures are insensitive to the order of training data and hence the final tree obtained is invariant to any permutation of the data. This leads to a serious limitation in modeling data instances that have order dependencies. In this work, we propose the use of Effort-To-Compress (ETC) - a complexity measure, for the first time, as an impurity measure. Unlike Shannon entropy and Gini impurity, structural impurity based on ETC is able to capture order dependencies in the data, thus obtaining potentially different decision trees for different permutations of the same data instances (Permutation Decision Trees). We then introduce the notion of Permutation Bagging achieved using permutation decision trees without the need for random feature selection and sub-sampling. We compare the performance of the proposed permutation bagged decision trees with Random Forests. Our model does not assume that the data instances are independent and identically distributed. Potential applications include scenarios where a temporal order present in the data instances is to be respected.

Cause-Effect Preservation and Classification using Neurochaos Learning

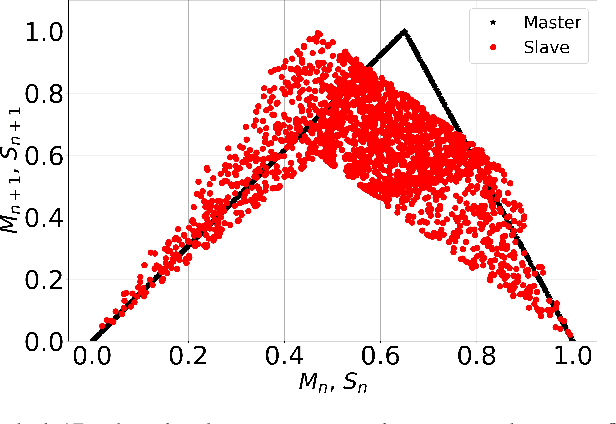
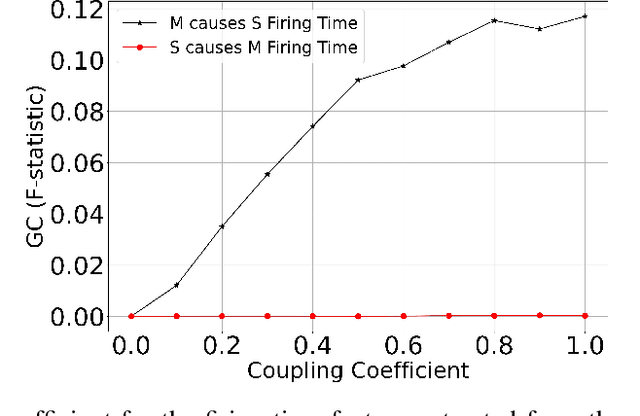
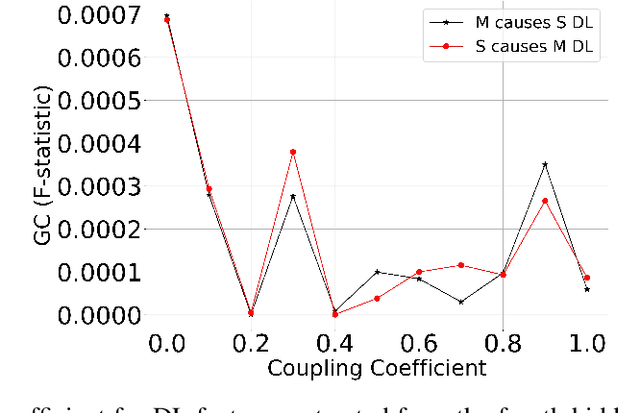
Discovering cause-effect from observational data is an important but challenging problem in science and engineering. In this work, a recently proposed brain inspired learning algorithm namely-\emph{Neurochaos Learning} (NL) is used for the classification of cause-effect from simulated data. The data instances used are generated from coupled AR processes, coupled 1D chaotic skew tent maps, coupled 1D chaotic logistic maps and a real-world prey-predator system. The proposed method consistently outperforms a five layer Deep Neural Network architecture for coupling coefficient values ranging from $0.1$ to $0.7$. Further, we investigate the preservation of causality in the feature extracted space of NL using Granger Causality (GC) for coupled AR processes and and Compression-Complexity Causality (CCC) for coupled chaotic systems and real-world prey-predator dataset. This ability of NL to preserve causality under a chaotic transformation and successfully classify cause and effect time series (including a transfer learning scenario) is highly desirable in causal machine learning applications.

A Novel Chaos Theory Inspired Neuronal Architecture

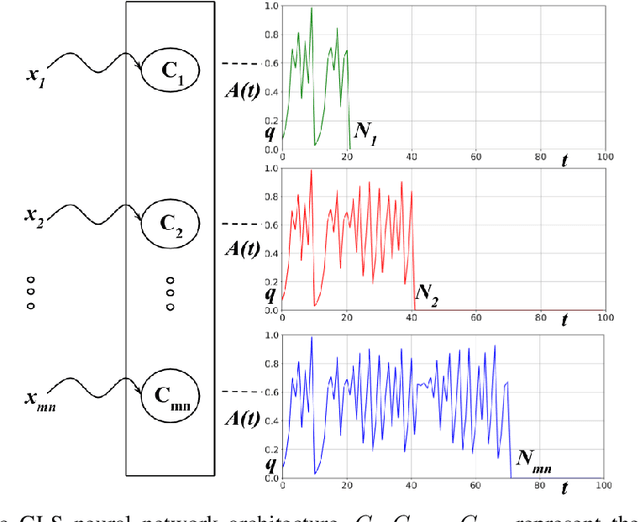
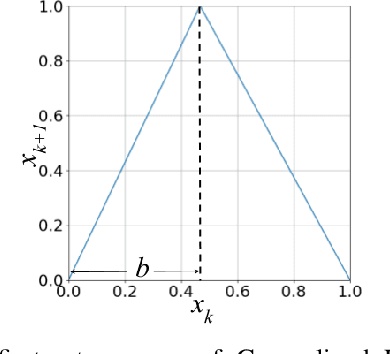
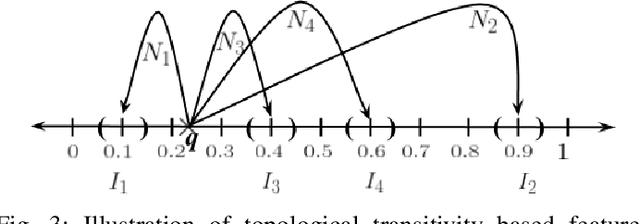
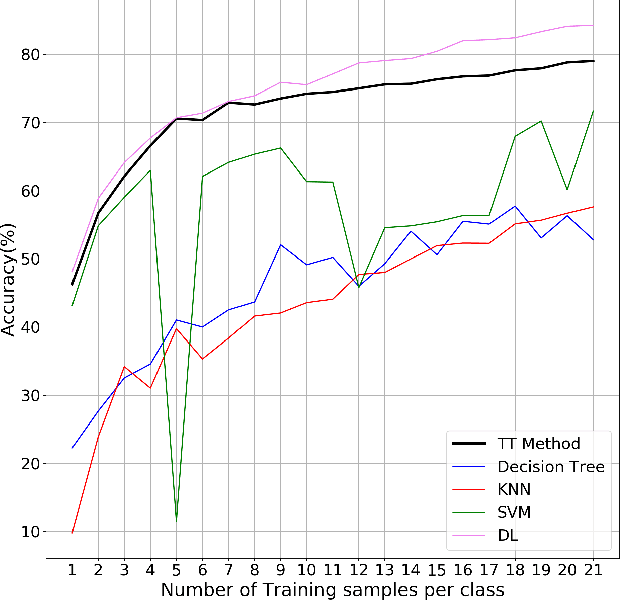
The practical success of widely used machine learning (ML) and deep learning (DL) algorithms in Artificial Intelligence (AI) community owes to availability of large datasets for training and huge computational resources. Despite the enormous practical success of AI, these algorithms are only loosely inspired from the biological brain and do not mimic any of the fundamental properties of neurons in the brain, one such property being the chaotic firing of biological neurons. This motivates us to develop a novel neuronal architecture where the individual neurons are intrinsically chaotic in nature. By making use of the topological transitivity property of chaos, our neuronal network is able to perform classification tasks with very less number of training samples. For the MNIST dataset, with as low as $0.1 \%$ of the total training data, our method outperforms ML and matches DL in classification accuracy for up to $7$ training samples/class. For the Iris dataset, our accuracy is comparable with ML algorithms, and even with just two training samples/class, we report an accuracy as high as $95.8 \%$. This work highlights the effectiveness of chaos and its properties for learning and paves the way for chaos-inspired neuronal architectures by closely mimicking the chaotic nature of neurons in the brain.