Permutation Decision Trees

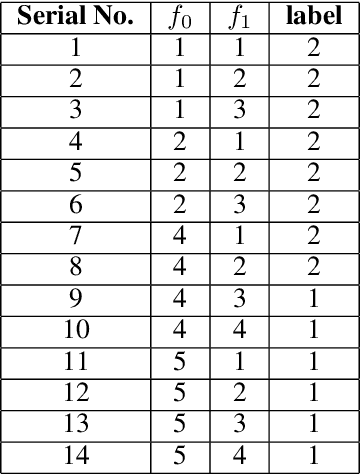
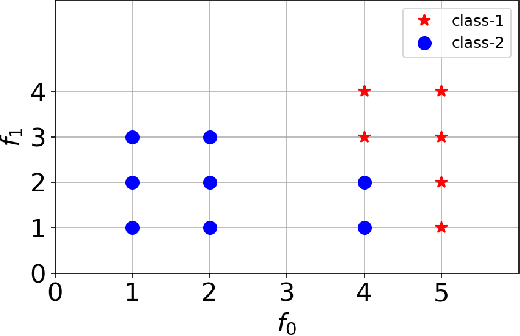
Decision Tree is a well understood Machine Learning model that is based on minimizing impurities in the internal nodes. The most common impurity measures are Shannon entropy and Gini impurity. These impurity measures are insensitive to the order of training data and hence the final tree obtained is invariant to any permutation of the data. This leads to a serious limitation in modeling data instances that have order dependencies. In this work, we propose the use of Effort-To-Compress (ETC) - a complexity measure, for the first time, as an impurity measure. Unlike Shannon entropy and Gini impurity, structural impurity based on ETC is able to capture order dependencies in the data, thus obtaining potentially different decision trees for different permutations of the same data instances (Permutation Decision Trees). We then introduce the notion of Permutation Bagging achieved using permutation decision trees without the need for random feature selection and sub-sampling. We compare the performance of the proposed permutation bagged decision trees with Random Forests. Our model does not assume that the data instances are independent and identically distributed. Potential applications include scenarios where a temporal order present in the data instances is to be respected.