Stein's unbiased risk estimate and Hyvärinen's score matching

We study two G-modeling strategies for estimating the signal distribution (the empirical Bayesian's prior) from observations corrupted with normal noise. First, we choose the signal distribution by minimizing Stein's unbiased risk estimate (SURE) of the implied Eddington/Tweedie Bayes denoiser, an approach motivated by optimal empirical Bayesian shrinkage estimation of the signals. Second, we select the signal distribution by minimizing Hyv\"arinen's score matching objective for the implied score (derivative of log-marginal density), targeting minimal Fisher divergence between estimated and true marginal densities. While these strategies appear distinct, they are known to be mathematically equivalent. We provide a unified analysis of SURE and score matching under both well-specified signal distribution classes and misspecification. In the classical well-specified setting with homoscedastic noise and compactly supported signal distribution, we establish nearly parametric rates of convergence of the empirical Bayes regret and the Fisher divergence. In a commonly studied misspecified model, we establish fast rates of convergence to the oracle denoiser and corresponding oracle inequalities. Our empirical results demonstrate competitiveness with nonparametric maximum likelihood in well-specified settings, while showing superior performance under misspecification, particularly in settings involving heteroscedasticity and side information.

Prediction-Powered Adaptive Shrinkage Estimation

Prediction-Powered Inference (PPI) is a powerful framework for enhancing statistical estimates by combining limited gold-standard data with machine learning (ML) predictions. While prior work has demonstrated PPI's benefits for individual statistical tasks, modern applications require answering numerous parallel statistical questions. We introduce Prediction-Powered Adaptive Shrinkage (PAS), a method that bridges PPI with empirical Bayes shrinkage to improve the estimation of multiple means. PAS debiases noisy ML predictions within each task and then borrows strength across tasks by using those same predictions as a reference point for shrinkage. The amount of shrinkage is determined by minimizing an unbiased estimate of risk, and we prove that this tuning strategy is asymptotically optimal. Experiments on both synthetic and real-world datasets show that PAS adapts to the reliability of the ML predictions and outperforms traditional and modern baselines in large-scale applications.

Net benefit, calibration, threshold selection, and training objectives for algorithmic fairness in healthcare

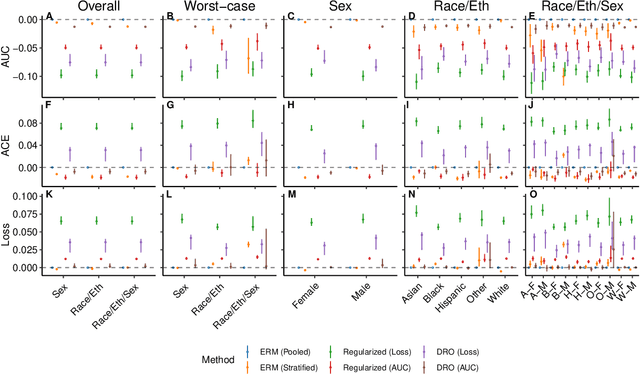
A growing body of work uses the paradigm of algorithmic fairness to frame the development of techniques to anticipate and proactively mitigate the introduction or exacerbation of health inequities that may follow from the use of model-guided decision-making. We evaluate the interplay between measures of model performance, fairness, and the expected utility of decision-making to offer practical recommendations for the operationalization of algorithmic fairness principles for the development and evaluation of predictive models in healthcare. We conduct an empirical case-study via development of models to estimate the ten-year risk of atherosclerotic cardiovascular disease to inform statin initiation in accordance with clinical practice guidelines. We demonstrate that approaches that incorporate fairness considerations into the model training objective typically do not improve model performance or confer greater net benefit for any of the studied patient populations compared to the use of standard learning paradigms followed by threshold selection concordant with patient preferences, evidence of intervention effectiveness, and model calibration. These results hold when the measured outcomes are not subject to differential measurement error across patient populations and threshold selection is unconstrained, regardless of whether differences in model performance metrics, such as in true and false positive error rates, are present. In closing, we argue for focusing model development efforts on developing calibrated models that predict outcomes well for all patient populations while emphasizing that such efforts are complementary to transparent reporting, participatory design, and reasoning about the impact of model-informed interventions in context.

Covariate-Powered Empirical Bayes Estimation

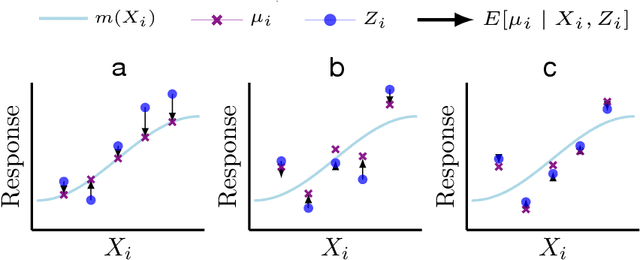
We study methods for simultaneous analysis of many noisy experiments in the presence of rich covariate information. The goal of the analyst is to optimally estimate the true effect underlying each experiment. Both the noisy experimental results and the auxiliary covariates are useful for this purpose, but neither data source on its own captures all the information available to the analyst. In this paper, we propose a flexible plug-in empirical Bayes estimator that synthesizes both sources of information and may leverage any black-box predictive model. We show that our approach is within a constant factor of minimax for a simple data-generating model. Furthermore, we establish robust convergence guarantees for our method that hold under considerable generality, and exhibit promising empirical performance on both real and simulated data.