Covariate-Powered Empirical Bayes Estimation
Paper and Code
Jun 04, 2019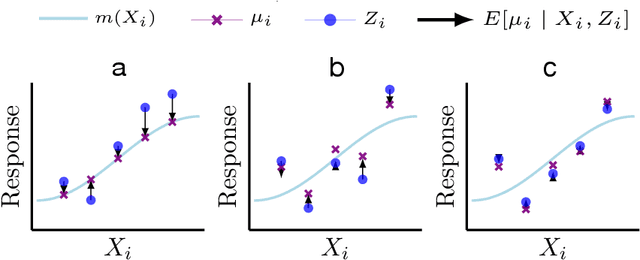


We study methods for simultaneous analysis of many noisy experiments in the presence of rich covariate information. The goal of the analyst is to optimally estimate the true effect underlying each experiment. Both the noisy experimental results and the auxiliary covariates are useful for this purpose, but neither data source on its own captures all the information available to the analyst. In this paper, we propose a flexible plug-in empirical Bayes estimator that synthesizes both sources of information and may leverage any black-box predictive model. We show that our approach is within a constant factor of minimax for a simple data-generating model. Furthermore, we establish robust convergence guarantees for our method that hold under considerable generality, and exhibit promising empirical performance on both real and simulated data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge