Automated Fetal Biometry Assessment with Deep Ensembles using Sparse-Sampling of 2D Intrapartum Ultrasound Images

The International Society of Ultrasound advocates Intrapartum Ultrasound (US) Imaging in Obstetrics and Gynecology (ISUOG) to monitor labour progression through changes in fetal head position. Two reliable ultrasound-derived parameters that are used to predict outcomes of instrumental vaginal delivery are the angle of progression (AoP) and head-symphysis distance (HSD). In this work, as part of the Intrapartum Ultrasounds Grand Challenge (IUGC) 2024, we propose an automated fetal biometry measurement pipeline to reduce intra- and inter-observer variability and improve measurement reliability. Our pipeline consists of three key tasks: (i) classification of standard planes (SP) from US videos, (ii) segmentation of fetal head and pubic symphysis from the detected SPs, and (iii) computation of the AoP and HSD from the segmented regions. We perform sparse sampling to mitigate class imbalances and reduce spurious correlations in task (i), and utilize ensemble-based deep learning methods for task (i) and (ii) to enhance generalizability under different US acquisition settings. Finally, to promote robustness in task iii) with respect to the structural fidelity of measurements, we retain the largest connected components and apply ellipse fitting to the segmentations. Our solution achieved ACC: 0.9452, F1: 0.9225, AUC: 0.983, MCC: 0.8361, DSC: 0.918, HD: 19.73, ASD: 5.71, $\Delta_{AoP}$: 8.90 and $\Delta_{HSD}$: 14.35 across an unseen hold-out set of 4 patients and 224 US frames. The results from the proposed automated pipeline can improve the understanding of labour arrest causes and guide the development of clinical risk stratification tools for efficient and effective prenatal care.

Exploring Test Time Adaptation for Subcortical Segmentation of the Fetal Brain in 3D Ultrasound

Monitoring the growth of subcortical regions of the fetal brain in ultrasound (US) images can help identify the presence of abnormal development. Manually segmenting these regions is a challenging task, but recent work has shown that it can be automated using deep learning. However, applying pretrained models to unseen freehand US volumes often leads to a degradation of performance due to the vast differences in acquisition and alignment. In this work, we first demonstrate that test time adaptation (TTA) can be used to improve model performance in the presence of both real and simulated domain shifts. We further propose a novel TTA method by incorporating a normative atlas as a prior for anatomy. In the presence of various types of domain shifts, we benchmark the performance of different TTA methods and demonstrate the improvements brought by our proposed approach, which may further facilitate automated monitoring of fetal brain development. Our code is available at https://github.com/joshuaomolegan/TTA-for-3D-Fetal-Subcortical-Segmentation.

Prototype Learning for Explainable Regression

The lack of explainability limits the adoption of deep learning models in clinical practice. While methods exist to improve the understanding of such models, these are mainly saliency-based and developed for classification, despite many important tasks in medical imaging being continuous regression problems. Therefore, in this work, we present ExPeRT: an explainable prototype-based model specifically designed for regression tasks. Our proposed model makes a sample prediction from the distances to a set of learned prototypes in latent space, using a weighted mean of prototype labels. The distances in latent space are regularized to be relative to label differences, and each of the prototypes can be visualized as a sample from the training set. The image-level distances are further constructed from patch-level distances, in which the patches of both images are structurally matched using optimal transport. We demonstrate our proposed model on the task of brain age prediction on two image datasets: adult MR and fetal ultrasound. Our approach achieved state-of-the-art prediction performance while providing insight in the model's reasoning process.

TEDS-Net: Enforcing Diffeomorphisms in Spatial Transformers to Guarantee Topology Preservation in Segmentations

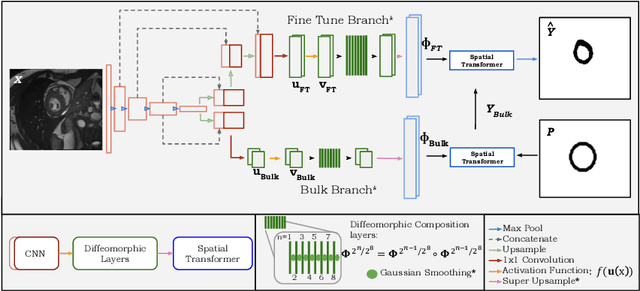
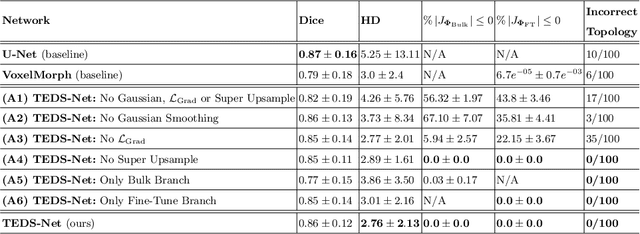
Accurate topology is key when performing meaningful anatomical segmentations, however, it is often overlooked in traditional deep learning methods. In this work we propose TEDS-Net: a novel segmentation method that guarantees accurate topology. Our method is built upon a continuous diffeomorphic framework, which enforces topology preservation. However, in practice, diffeomorphic fields are represented using a finite number of parameters and sampled using methods such as linear interpolation, violating the theoretical guarantees. We therefore introduce additional modifications to more strictly enforce it. Our network learns how to warp a binary prior, with the desired topological characteristics, to complete the segmentation task. We tested our method on myocardium segmentation from an open-source 2D heart dataset. TEDS-Net preserved topology in 100% of the cases, compared to 90% from the U-Net, without sacrificing on Hausdorff Distance or Dice performance. Code will be made available at: www.github.com/mwyburd/TEDS-Net