Robust Neural Regression via Uncertainty Learning

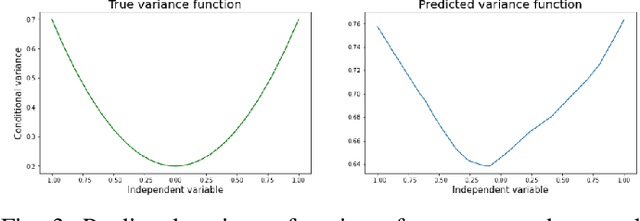
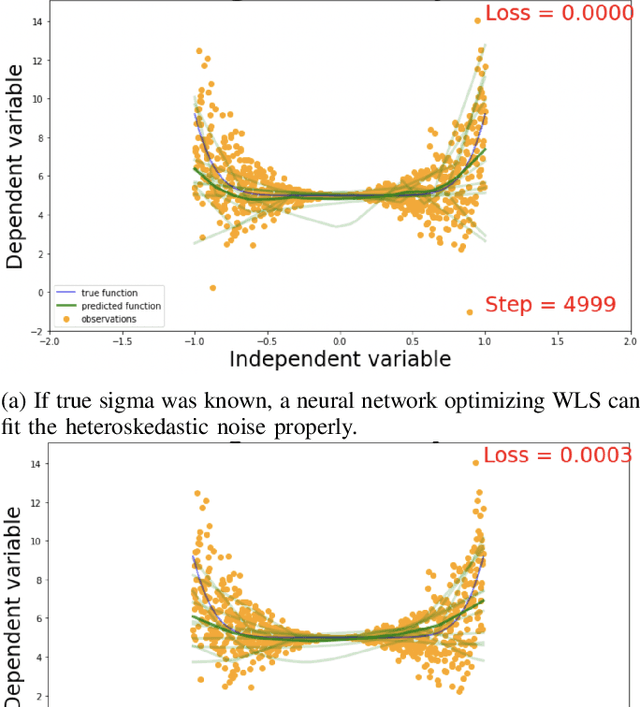
Deep neural networks tend to underestimate uncertainty and produce overly confident predictions. Recently proposed solutions, such as MC Dropout and SDENet, require complex training and/or auxiliary out-of-distribution data. We propose a simple solution by extending the time-tested iterative reweighted least square (IRLS) in generalised linear regression. We use two sub-networks to parametrise the prediction and uncertainty estimation, enabling easy handling of complex inputs and nonlinear response. The two sub-networks have shared representations and are trained via two complementary loss functions for the prediction and the uncertainty estimates, with interleaving steps as in a cooperative game. Compared with more complex models such as MC-Dropout or SDE-Net, our proposed network is simpler to implement and more robust (insensitive to varying aleatoric and epistemic uncertainty).

On the Inter-relationships among Drift rate, Forgetting rate, Bias/variance profile and Error

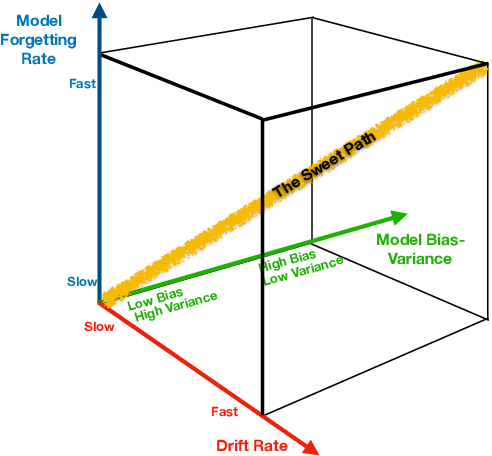
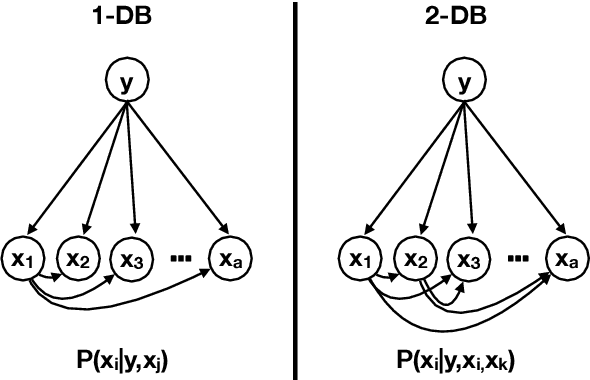
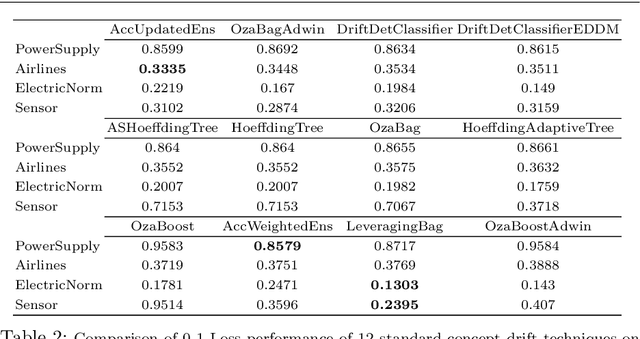
We propose two general and falsifiable hypotheses about expectations on generalization error when learning in the context of concept drift. One posits that as drift rate increases, the forgetting rate that minimizes generalization error will also increase and vice versa. The other posits that as a learner's forgetting rate increases, the bias/variance profile that minimizes generalization error will have lower variance and vice versa. These hypotheses lead to the concept of the sweet path, a path through the 3-d space of alternative drift rates, forgetting rates and bias/variance profiles on which generalization error will be minimized, such that slow drift is coupled with low forgetting and low bias, while rapid drift is coupled with fast forgetting and low variance. We present experiments that support the existence of such a sweet path. We also demonstrate that simple learners that select appropriate forgetting rates and bias/variance profiles are highly competitive with the state-of-the-art in incremental learners for concept drift on real-world drift problems.

On the Effectiveness of Discretizing Quantitative Attributes in Linear Classifiers

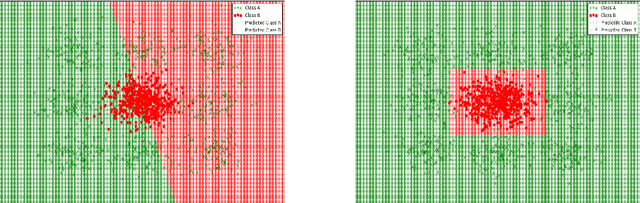
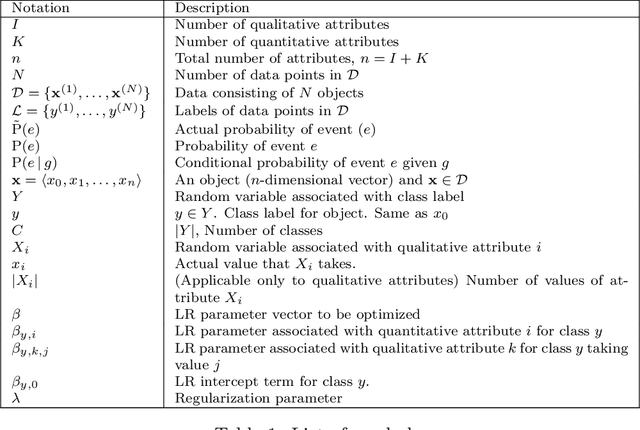
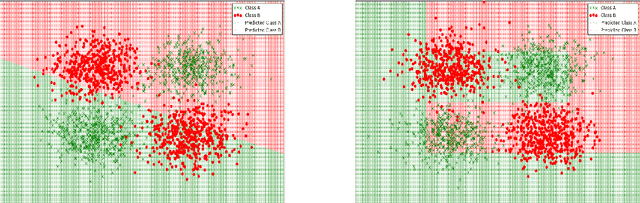
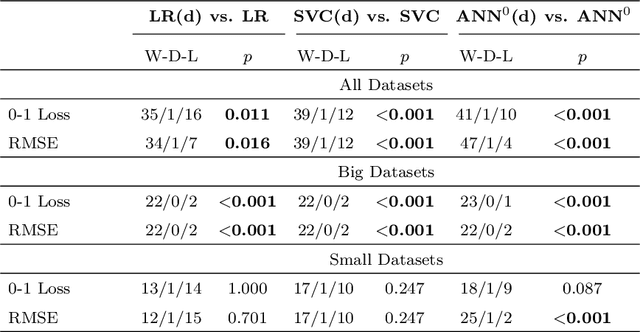
Learning algorithms that learn linear models often have high representation bias on real-world problems. In this paper, we show that this representation bias can be greatly reduced by discretization. Discretization is a common procedure in machine learning that is used to convert a quantitative attribute into a qualitative one. It is often motivated by the limitation of some learners to qualitative data. Discretization loses information, as fewer distinctions between instances are possible using discretized data relative to undiscretized data. In consequence, where discretization is not essential, it might appear desirable to avoid it. However, it has been shown that discretization often substantially reduces the error of the linear generative Bayesian classifier naive Bayes. This motivates a systematic study of the effectiveness of discretizing quantitative attributes for other linear classifiers. In this work, we study the effect of discretization on the performance of linear classifiers optimizing three distinct discriminative objective functions --- logistic regression (optimizing negative log-likelihood), support vector classifiers (optimizing hinge loss) and a zero-hidden layer artificial neural network (optimizing mean-square-error). We show that discretization can greatly increase the accuracy of these linear discriminative learners by reducing their representation bias, especially on big datasets. We substantiate our claims with an empirical study on $42$ benchmark datasets.

Deep Broad Learning - Big Models for Big Data

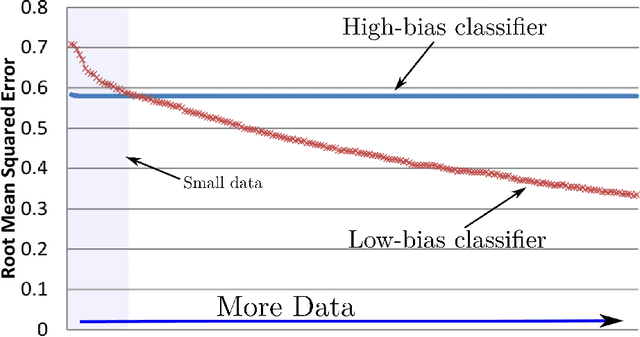
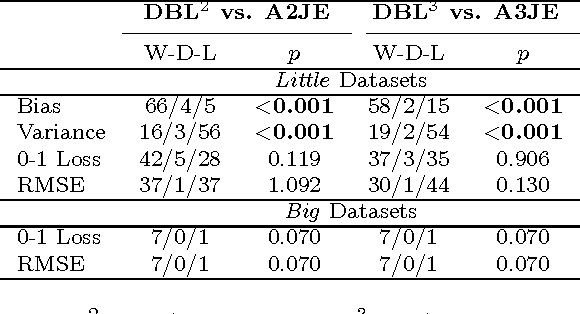
Deep learning has demonstrated the power of detailed modeling of complex high-order (multivariate) interactions in data. For some learning tasks there is power in learning models that are not only Deep but also Broad. By Broad, we mean models that incorporate evidence from large numbers of features. This is of especial value in applications where many different features and combinations of features all carry small amounts of information about the class. The most accurate models will integrate all that information. In this paper, we propose an algorithm for Deep Broad Learning called DBL. The proposed algorithm has a tunable parameter $n$, that specifies the depth of the model. It provides straightforward paths towards out-of-core learning for large data. We demonstrate that DBL learns models from large quantities of data with accuracy that is highly competitive with the state-of-the-art.