On the Effectiveness of Discretizing Quantitative Attributes in Linear Classifiers
Paper and Code
Jan 24, 2017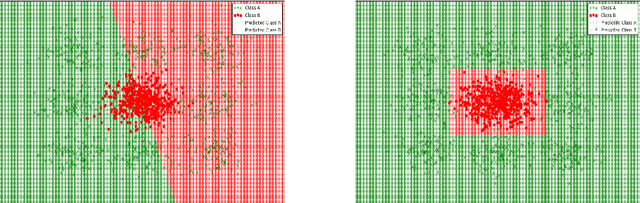
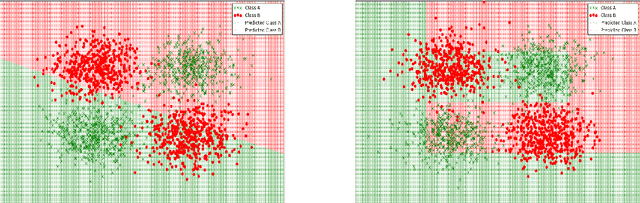
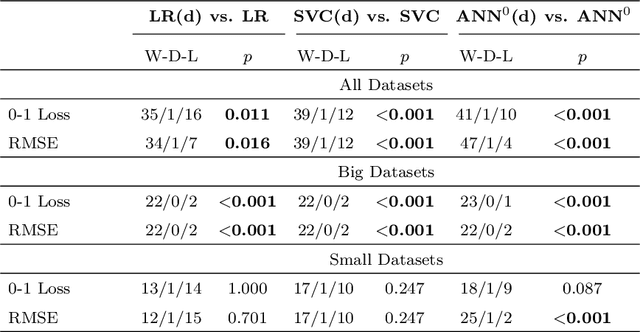
Learning algorithms that learn linear models often have high representation bias on real-world problems. In this paper, we show that this representation bias can be greatly reduced by discretization. Discretization is a common procedure in machine learning that is used to convert a quantitative attribute into a qualitative one. It is often motivated by the limitation of some learners to qualitative data. Discretization loses information, as fewer distinctions between instances are possible using discretized data relative to undiscretized data. In consequence, where discretization is not essential, it might appear desirable to avoid it. However, it has been shown that discretization often substantially reduces the error of the linear generative Bayesian classifier naive Bayes. This motivates a systematic study of the effectiveness of discretizing quantitative attributes for other linear classifiers. In this work, we study the effect of discretization on the performance of linear classifiers optimizing three distinct discriminative objective functions --- logistic regression (optimizing negative log-likelihood), support vector classifiers (optimizing hinge loss) and a zero-hidden layer artificial neural network (optimizing mean-square-error). We show that discretization can greatly increase the accuracy of these linear discriminative learners by reducing their representation bias, especially on big datasets. We substantiate our claims with an empirical study on $42$ benchmark datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge