On the Inter-relationships among Drift rate, Forgetting rate, Bias/variance profile and Error
Paper and Code
Feb 04, 2018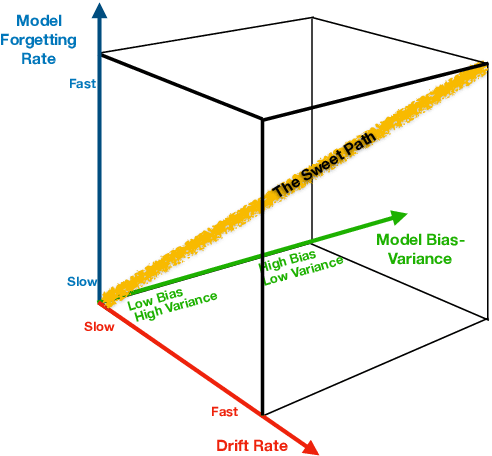
We propose two general and falsifiable hypotheses about expectations on generalization error when learning in the context of concept drift. One posits that as drift rate increases, the forgetting rate that minimizes generalization error will also increase and vice versa. The other posits that as a learner's forgetting rate increases, the bias/variance profile that minimizes generalization error will have lower variance and vice versa. These hypotheses lead to the concept of the sweet path, a path through the 3-d space of alternative drift rates, forgetting rates and bias/variance profiles on which generalization error will be minimized, such that slow drift is coupled with low forgetting and low bias, while rapid drift is coupled with fast forgetting and low variance. We present experiments that support the existence of such a sweet path. We also demonstrate that simple learners that select appropriate forgetting rates and bias/variance profiles are highly competitive with the state-of-the-art in incremental learners for concept drift on real-world drift problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge