Framework for Evaluating Faithfulness of Local Explanations

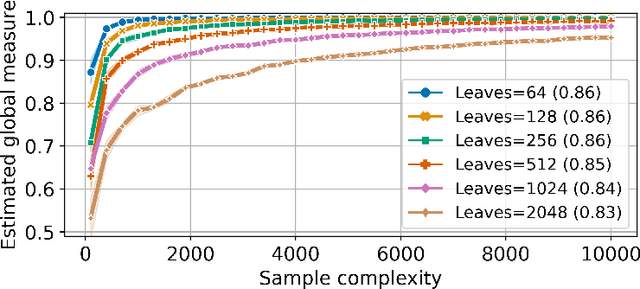
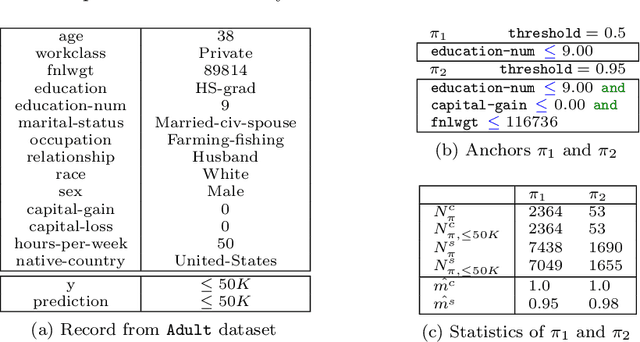
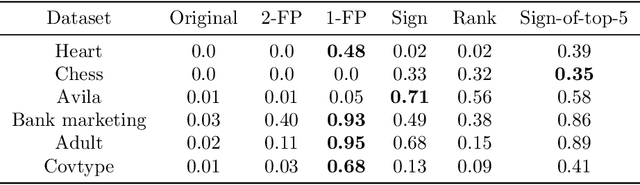
We study the faithfulness of an explanation system to the underlying prediction model. We show that this can be captured by two properties, consistency and sufficiency, and introduce quantitative measures of the extent to which these hold. Interestingly, these measures depend on the test-time data distribution. For a variety of existing explanation systems, such as anchors, we analytically study these quantities. We also provide estimators and sample complexity bounds for empirically determining the faithfulness of black-box explanation systems. Finally, we experimentally validate the new properties and estimators.

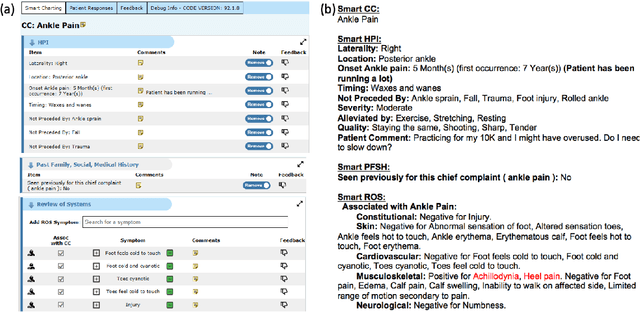
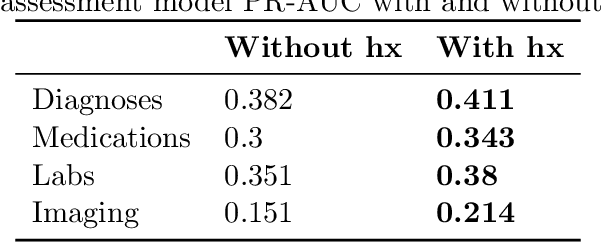
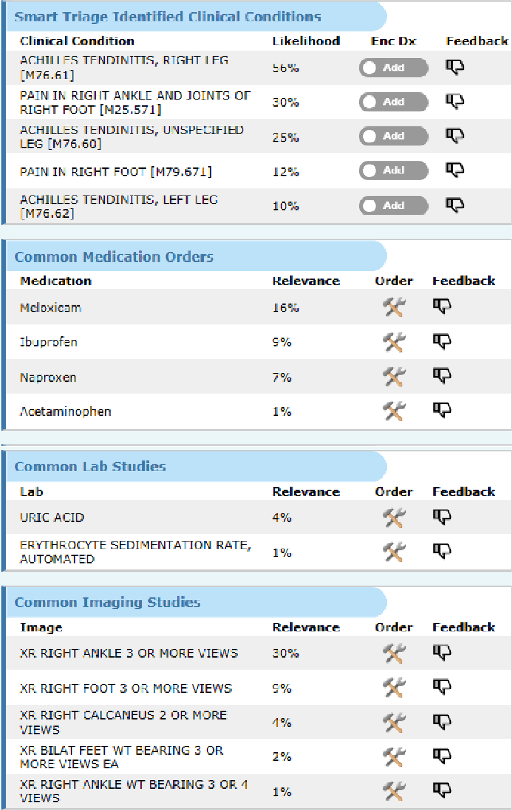
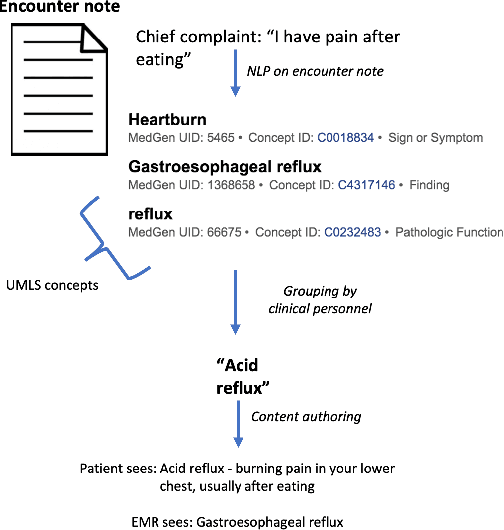
SmartTriage: A system for personalized patient data capture, documentation generation, and decision support

Symptom checkers have emerged as an important tool for collecting symptoms and diagnosing patients, minimizing the involvement of clinical personnel. We developed a machine-learning-backed system, SmartTriage, which goes beyond conventional symptom checking through a tight bi-directional integration with the electronic medical record (EMR). Conditioned on EMR-derived patient history, our system identifies the patient's chief complaint from a free-text entry and then asks a series of discrete questions to obtain relevant symptomatology. The patient-specific data are used to predict detailed ICD-10-CM codes as well as medication, laboratory, and imaging orders. Patient responses and clinical decision support (CDS) predictions are then inserted back into the EMR. To train the machine learning components of SmartTriage, we employed novel data sets of over 25 million primary care encounters and 1 million patient free-text reason-for-visit entries. These data sets were used to construct: (1) a long short-term memory (LSTM) based patient history representation, (2) a fine-tuned transformer model for chief complaint extraction, (3) a random forest model for question sequencing, and (4) a feed-forward network for CDS predictions. We also present the full production architecture for the pilot deployment of SmartTriage that covers 337 patient chief complaints.

ExKMC: Expanding Explainable $k$-Means Clustering

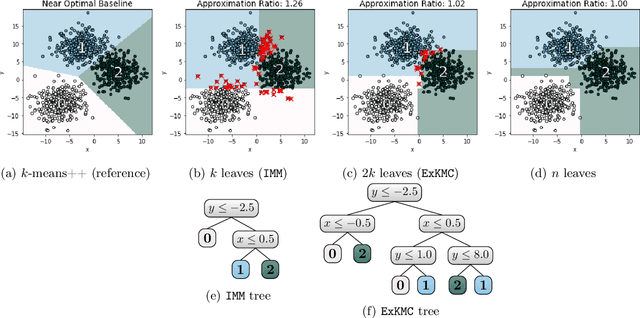
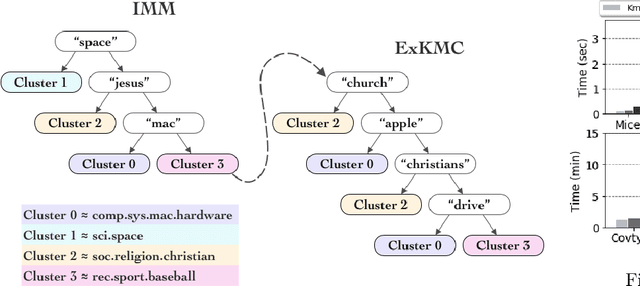
Despite the popularity of explainable AI, there is limited work on effective methods for unsupervised learning. We study algorithms for $k$-means clustering, focusing on a trade-off between explainability and accuracy. Following prior work, we use a small decision tree to partition a dataset into $k$ clusters. This enables us to explain each cluster assignment by a short sequence of single-feature thresholds. While larger trees produce more accurate clusterings, they also require more complex explanations. To allow flexibility, we develop a new explainable $k$-means clustering algorithm, ExKMC, that takes an additional parameter $k' \geq k$ and outputs a decision tree with $k'$ leaves. We use a new surrogate cost to efficiently expand the tree and to label the leaves with one of $k$ clusters. We prove that as $k'$ increases, the surrogate cost is non-increasing, and hence, we trade explainability for accuracy. Empirically, we validate that ExKMC produces a low cost clustering, outperforming both standard decision tree methods and other algorithms for explainable clustering. Implementation of ExKMC available at https://github.com/navefr/ExKMC.

Explainable $k$-Means and $k$-Medians Clustering

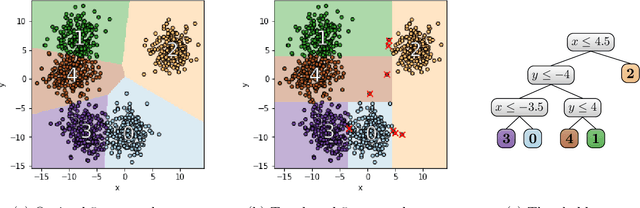
Clustering is a popular form of unsupervised learning for geometric data. Unfortunately, many clustering algorithms lead to cluster assignments that are hard to explain, partially because they depend on all the features of the data in a complicated way. To improve interpretability, we consider using a small decision tree to partition a data set into clusters, so that clusters can be characterized in a straightforward manner. We study this problem from a theoretical viewpoint, measuring cluster quality by the $k$-means and $k$-medians objectives: Must there exist a tree-induced clustering whose cost is comparable to that of the best unconstrained clustering, and if so, how can it be found? In terms of negative results, we show, first, that popular top-down decision tree algorithms may lead to clusterings with arbitrarily large cost, and second, that any tree-induced clustering must in general incur an $\Omega(\log k)$ approximation factor compared to the optimal clustering. On the positive side, we design an efficient algorithm that produces explainable clusters using a tree with $k$ leaves. For two means/medians, we show that a single threshold cut suffices to achieve a constant factor approximation, and we give nearly-matching lower bounds. For general $k \geq 2$, our algorithm is an $O(k)$ approximation to the optimal $k$-medians and an $O(k^2)$ approximation to the optimal $k$-means. Prior to our work, no algorithms were known with provable guarantees independent of dimension and input size.