Explainable $k$-Means and $k$-Medians Clustering
Paper and Code
Feb 28, 2020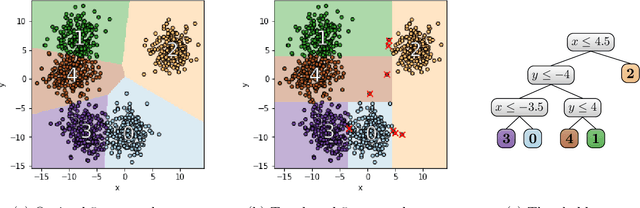


Clustering is a popular form of unsupervised learning for geometric data. Unfortunately, many clustering algorithms lead to cluster assignments that are hard to explain, partially because they depend on all the features of the data in a complicated way. To improve interpretability, we consider using a small decision tree to partition a data set into clusters, so that clusters can be characterized in a straightforward manner. We study this problem from a theoretical viewpoint, measuring cluster quality by the $k$-means and $k$-medians objectives: Must there exist a tree-induced clustering whose cost is comparable to that of the best unconstrained clustering, and if so, how can it be found? In terms of negative results, we show, first, that popular top-down decision tree algorithms may lead to clusterings with arbitrarily large cost, and second, that any tree-induced clustering must in general incur an $\Omega(\log k)$ approximation factor compared to the optimal clustering. On the positive side, we design an efficient algorithm that produces explainable clusters using a tree with $k$ leaves. For two means/medians, we show that a single threshold cut suffices to achieve a constant factor approximation, and we give nearly-matching lower bounds. For general $k \geq 2$, our algorithm is an $O(k)$ approximation to the optimal $k$-medians and an $O(k^2)$ approximation to the optimal $k$-means. Prior to our work, no algorithms were known with provable guarantees independent of dimension and input size.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge