Final Report for CHESS: Cloud, High-Performance Computing, and Edge for Science and Security

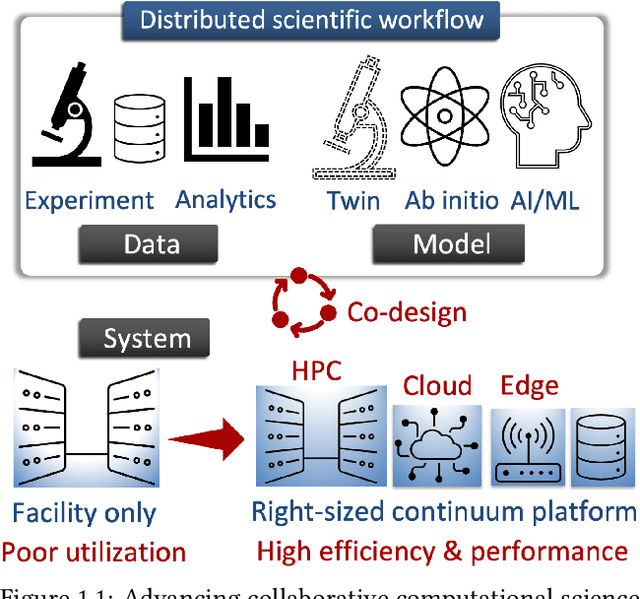
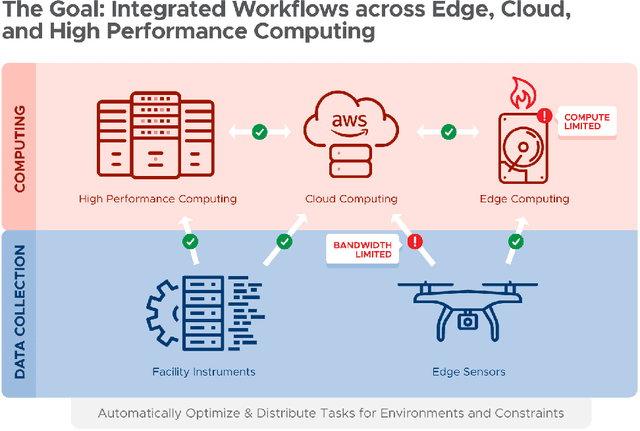
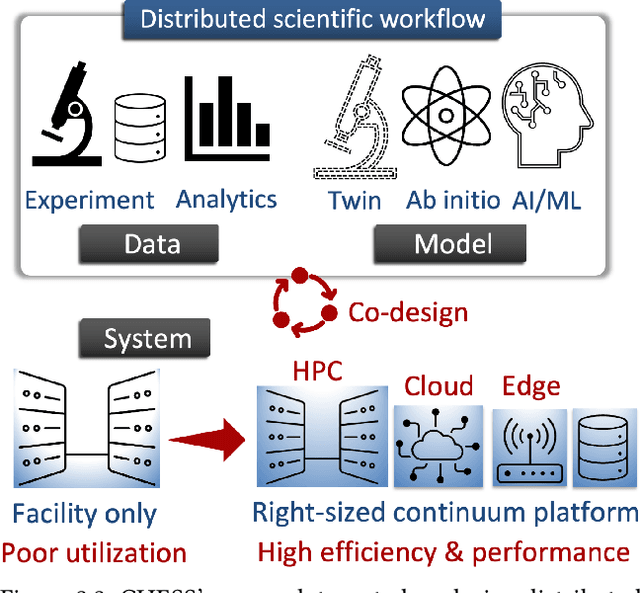
Automating the theory-experiment cycle requires effective distributed workflows that utilize a computing continuum spanning lab instruments, edge sensors, computing resources at multiple facilities, data sets distributed across multiple information sources, and potentially cloud. Unfortunately, the obvious methods for constructing continuum platforms, orchestrating workflow tasks, and curating datasets over time fail to achieve scientific requirements for performance, energy, security, and reliability. Furthermore, achieving the best use of continuum resources depends upon the efficient composition and execution of workflow tasks, i.e., combinations of numerical solvers, data analytics, and machine learning. Pacific Northwest National Laboratory's LDRD "Cloud, High-Performance Computing (HPC), and Edge for Science and Security" (CHESS) has developed a set of interrelated capabilities for enabling distributed scientific workflows and curating datasets. This report describes the results and successes of CHESS from the perspective of open science.

OPDR: Order-Preserving Dimension Reduction for Semantic Embedding of Multimodal Scientific Data

One of the most common operations in multimodal scientific data management is searching for the $k$ most similar items (or, $k$-nearest neighbors, KNN) from the database after being provided a new item. Although recent advances of multimodal machine learning models offer a \textit{semantic} index, the so-called \textit{embedding vectors} mapped from the original multimodal data, the dimension of the resulting embedding vectors are usually on the order of hundreds or a thousand, which are impractically high for time-sensitive scientific applications. This work proposes to reduce the dimensionality of the output embedding vectors such that the set of top-$k$ nearest neighbors do not change in the lower-dimensional space, namely Order-Preserving Dimension Reduction (OPDR). In order to develop such an OPDR method, our central hypothesis is that by analyzing the intrinsic relationship among key parameters during the dimension-reduction map, a quantitative function may be constructed to reveal the correlation between the target (lower) dimensionality and other variables. To demonstrate the hypothesis, this paper first defines a formal measure function to quantify the KNN similarity for a specific vector, then extends the measure into an aggregate accuracy of the global metric spaces, and finally derives a closed-form function between the target (lower) dimensionality and other variables. We incorporate the closed-function into popular dimension-reduction methods, various distance metrics, and embedding models.