Random Smoothing Might be Unable to Certify $\ell_\infty$ Robustness for High-Dimensional Images

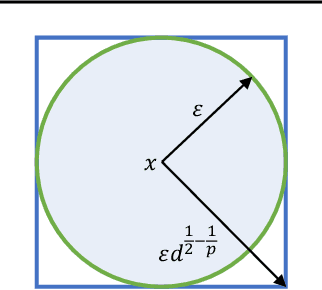
We show a hardness result for random smoothing to achieve certified adversarial robustness against attacks in the $\ell_p$ ball of radius $\epsilon$ when $p>2$. Although random smoothing has been well understood for the $\ell_2$ case using the Gaussian distribution, much remains unknown concerning the existence of a noise distribution that works for the case of $p>2$. This has been posed as an open problem by Cohen et al. (2019) and includes many significant paradigms such as the $\ell_\infty$ threat model. In this work, we show that any noise distribution $\mathcal{D}$ over $\mathbb{R}^d$ that provides $\ell_p$ robustness for all base classifiers with $p>2$ must satisfy $\mathbb{E}\eta_i^2=\Omega(d^{1-2/p}\epsilon^2(1-\delta)/\delta^2)$ for 99% of the features (pixels) of vector $\eta\sim\mathcal{D}$, where $\epsilon$ is the robust radius and $\delta$ is the score gap between the highest-scored class and the runner-up. Therefore, for high-dimensional images with pixel values bounded in $[0,255]$, the required noise will eventually dominate the useful information in the images, leading to trivial smoothed classifiers.

Quantifying Perceptual Distortion of Adversarial Examples

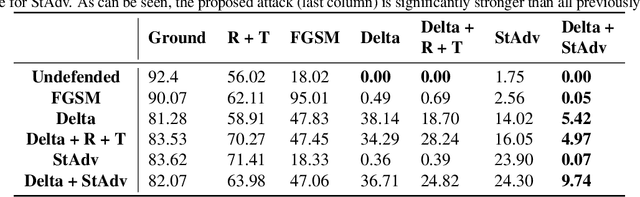
Recent work has shown that additive threat models, which only permit the addition of bounded noise to the pixels of an image, are insufficient for fully capturing the space of imperceivable adversarial examples. For example, small rotations and spatial transformations can fool classifiers, remain imperceivable to humans, but have large additive distance from the original images. In this work, we leverage quantitative perceptual metrics like LPIPS and SSIM to define a novel threat model for adversarial attacks. To demonstrate the value of quantifying the perceptual distortion of adversarial examples, we present and employ a unifying framework fusing different attack styles. We first prove that our framework results in images that are unattainable by attack styles in isolation. We then perform adversarial training using attacks generated by our framework to demonstrate that networks are only robust to classes of adversarial perturbations they have been trained against, and combination attacks are stronger than any of their individual components. Finally, we experimentally demonstrate that our combined attacks retain the same perceptual distortion but induce far higher misclassification rates when compared against individual attacks.