Parallel Gaussian Process Regression with Low-Rank Covariance Matrix Approximations

Gaussian processes (GP) are Bayesian non-parametric models that are widely used for probabilistic regression. Unfortunately, it cannot scale well with large data nor perform real-time predictions due to its cubic time cost in the data size. This paper presents two parallel GP regression methods that exploit low-rank covariance matrix approximations for distributing the computational load among parallel machines to achieve time efficiency and scalability. We theoretically guarantee the predictive performances of our proposed parallel GPs to be equivalent to that of some centralized approximate GP regression methods: The computation of their centralized counterparts can be distributed among parallel machines, hence achieving greater time efficiency and scalability. We analytically compare the properties of our parallel GPs such as time, space, and communication complexity. Empirical evaluation on two real-world datasets in a cluster of 20 computing nodes shows that our parallel GPs are significantly more time-efficient and scalable than their centralized counterparts and exact/full GP while achieving predictive performances comparable to full GP.

Multi-Robot Informative Path Planning for Active Sensing of Environmental Phenomena: A Tale of Two Algorithms

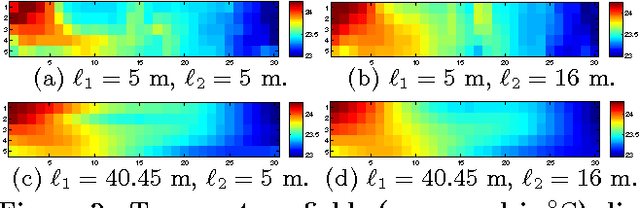
A key problem of robotic environmental sensing and monitoring is that of active sensing: How can a team of robots plan the most informative observation paths to minimize the uncertainty in modeling and predicting an environmental phenomenon? This paper presents two principled approaches to efficient information-theoretic path planning based on entropy and mutual information criteria for in situ active sensing of an important broad class of widely-occurring environmental phenomena called anisotropic fields. Our proposed algorithms are novel in addressing a trade-off between active sensing performance and time efficiency. An important practical consequence is that our algorithms can exploit the spatial correlation structure of Gaussian process-based anisotropic fields to improve time efficiency while preserving near-optimal active sensing performance. We analyze the time complexity of our algorithms and prove analytically that they scale better than state-of-the-art algorithms with increasing planning horizon length. We provide theoretical guarantees on the active sensing performance of our algorithms for a class of exploration tasks called transect sampling, which, in particular, can be improved with longer planning time and/or lower spatial correlation along the transect. Empirical evaluation on real-world anisotropic field data shows that our algorithms can perform better or at least as well as the state-of-the-art algorithms while often incurring a few orders of magnitude less computational time, even when the field conditions are less favorable.