Decentralized High-Dimensional Bayesian Optimization with Factor Graphs

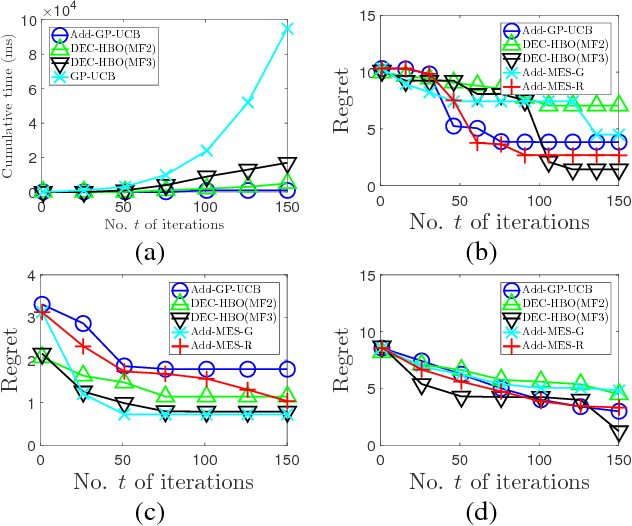
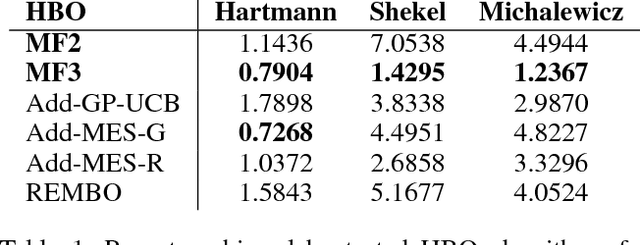
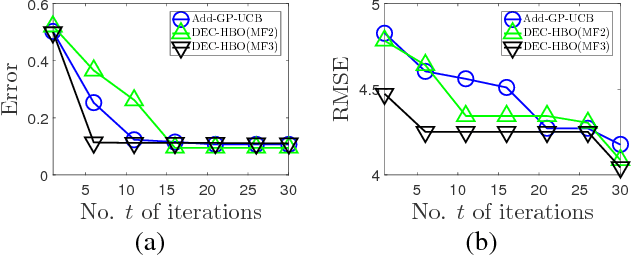
This paper presents a novel decentralized high-dimensional Bayesian optimization (DEC-HBO) algorithm that, in contrast to existing HBO algorithms, can exploit the interdependent effects of various input components on the output of the unknown objective function f for boosting the BO performance and still preserve scalability in the number of input dimensions without requiring prior knowledge or the existence of a low (effective) dimension of the input space. To realize this, we propose a sparse yet rich factor graph representation of f to be exploited for designing an acquisition function that can be similarly represented by a sparse factor graph and hence be efficiently optimized in a decentralized manner using distributed message passing. Despite richly characterizing the interdependent effects of the input components on the output of f with a factor graph, DEC-HBO can still guarantee no-regret performance asymptotically. Empirical evaluation on synthetic and real-world experiments (e.g., sparse Gaussian process model with 1811 hyperparameters) shows that DEC-HBO outperforms the state-of-the-art HBO algorithms.

Gaussian Process Decentralized Data Fusion Meets Transfer Learning in Large-Scale Distributed Cooperative Perception

This paper presents novel Gaussian process decentralized data fusion algorithms exploiting the notion of agent-centric support sets for distributed cooperative perception of large-scale environmental phenomena. To overcome the limitations of scale in existing works, our proposed algorithms allow every mobile sensing agent to choose a different support set and dynamically switch to another during execution for encapsulating its own data into a local summary that, perhaps surprisingly, can still be assimilated with the other agents' local summaries (i.e., based on their current choices of support sets) into a globally consistent summary to be used for predicting the phenomenon. To achieve this, we propose a novel transfer learning mechanism for a team of agents capable of sharing and transferring information encapsulated in a summary based on a support set to that utilizing a different support set with some loss that can be theoretically bounded and analyzed. To alleviate the issue of information loss accumulating over multiple instances of transfer learning, we propose a new information sharing mechanism to be incorporated into our algorithms in order to achieve memory-efficient lazy transfer learning. Empirical evaluation on real-world datasets show that our algorithms outperform the state-of-the-art methods.

Parallel Gaussian Process Regression with Low-Rank Covariance Matrix Approximations

Gaussian processes (GP) are Bayesian non-parametric models that are widely used for probabilistic regression. Unfortunately, it cannot scale well with large data nor perform real-time predictions due to its cubic time cost in the data size. This paper presents two parallel GP regression methods that exploit low-rank covariance matrix approximations for distributing the computational load among parallel machines to achieve time efficiency and scalability. We theoretically guarantee the predictive performances of our proposed parallel GPs to be equivalent to that of some centralized approximate GP regression methods: The computation of their centralized counterparts can be distributed among parallel machines, hence achieving greater time efficiency and scalability. We analytically compare the properties of our parallel GPs such as time, space, and communication complexity. Empirical evaluation on two real-world datasets in a cluster of 20 computing nodes shows that our parallel GPs are significantly more time-efficient and scalable than their centralized counterparts and exact/full GP while achieving predictive performances comparable to full GP.