Revisiting the Sample Complexity of Sparse Spectrum Approximation of Gaussian Processes

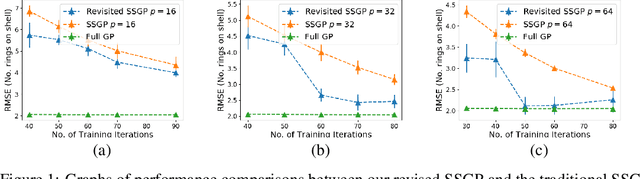
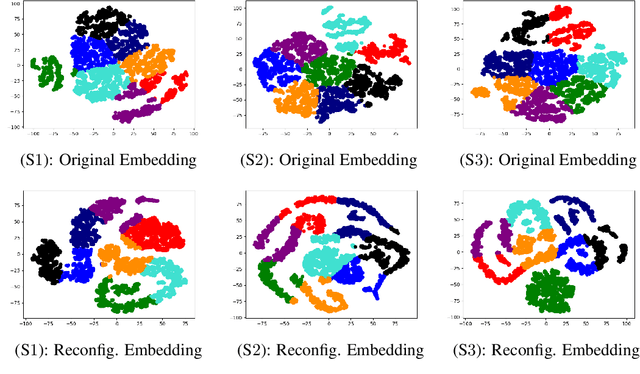
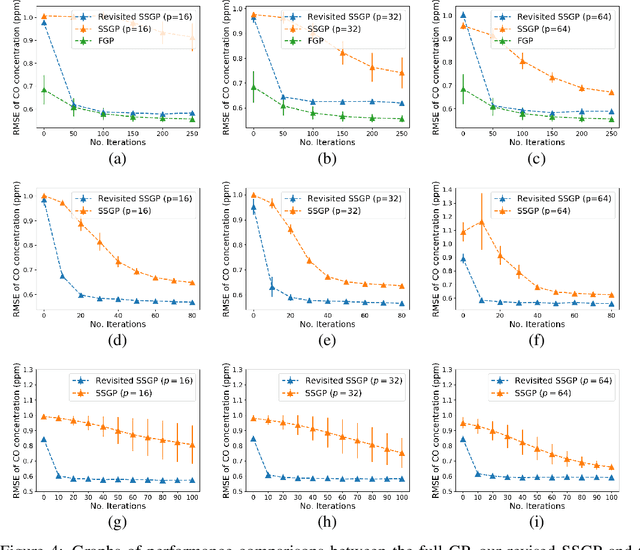
We introduce a new scalable approximation for Gaussian processes with provable guarantees which hold simultaneously over its entire parameter space. Our approximation is obtained from an improved sample complexity analysis for sparse spectrum Gaussian processes (SSGPs). In particular, our analysis shows that under a certain data disentangling condition, an SSGP's prediction and model evidence (for training) can well-approximate those of a full GP with low sample complexity. We also develop a new auto-encoding algorithm that finds a latent space to disentangle latent input coordinates into well-separated clusters, which is amenable to our sample complexity analysis. We validate our proposed method on several benchmarks with promising results supporting our theoretical analysis.

Collective Online Learning via Decentralized Gaussian Processes in Massive Multi-Agent Systems

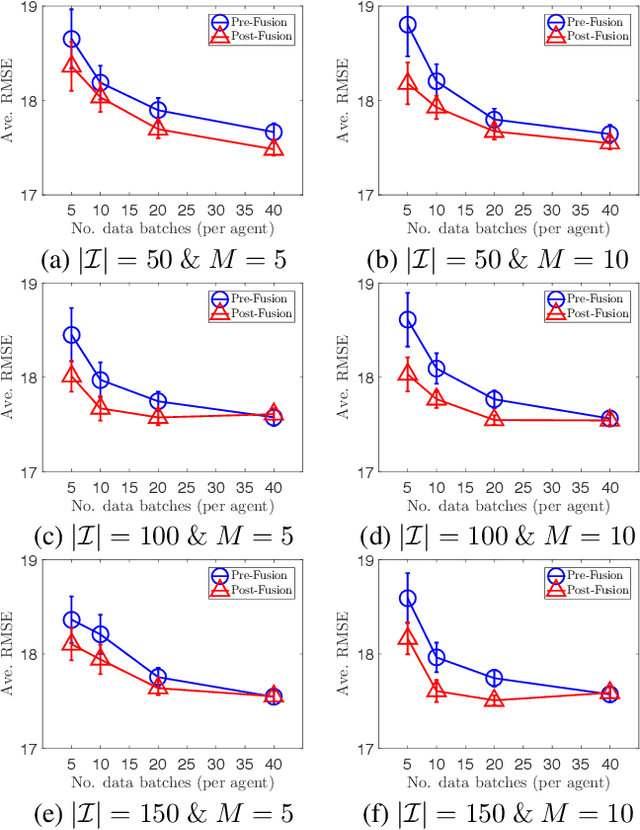
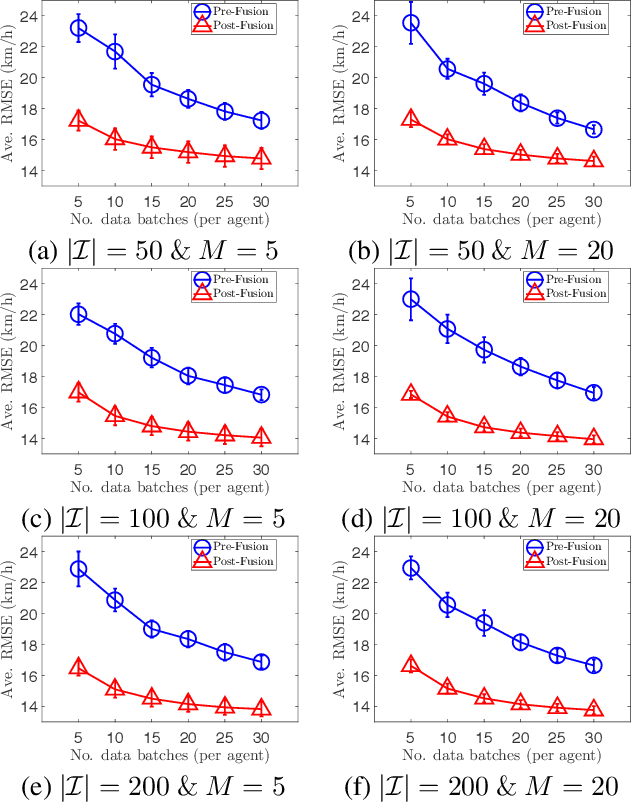
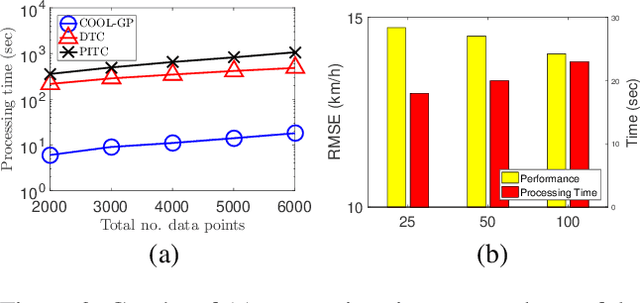
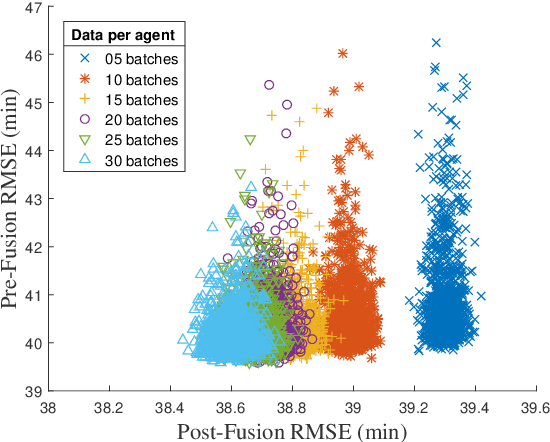
Distributed machine learning (ML) is a modern computation paradigm that divides its workload into independent tasks that can be simultaneously achieved by multiple machines (i.e., agents) for better scalability. However, a typical distributed system is usually implemented with a central server that collects data statistics from multiple independent machines operating on different subsets of data to build a global analytic model. This centralized communication architecture however exposes a single choke point for operational failure and places severe bottlenecks on the server's communication and computation capacities as it has to process a growing volume of communication from a crowd of learning agents. To mitigate these bottlenecks, this paper introduces a novel Collective Online Learning Gaussian Process framework for massive distributed systems that allows each agent to build its local model, which can be exchanged and combined efficiently with others via peer-to-peer communication to converge on a global model of higher quality. Finally, our empirical results consistently demonstrate the efficiency of our framework on both synthetic and real-world datasets.

Decentralized High-Dimensional Bayesian Optimization with Factor Graphs

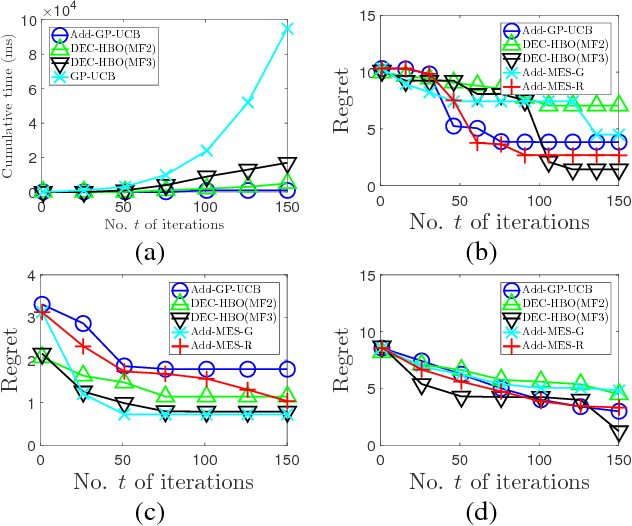
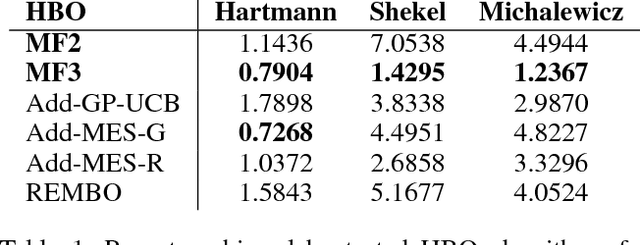
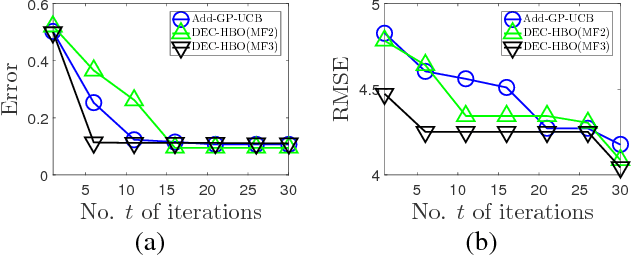
This paper presents a novel decentralized high-dimensional Bayesian optimization (DEC-HBO) algorithm that, in contrast to existing HBO algorithms, can exploit the interdependent effects of various input components on the output of the unknown objective function f for boosting the BO performance and still preserve scalability in the number of input dimensions without requiring prior knowledge or the existence of a low (effective) dimension of the input space. To realize this, we propose a sparse yet rich factor graph representation of f to be exploited for designing an acquisition function that can be similarly represented by a sparse factor graph and hence be efficiently optimized in a decentralized manner using distributed message passing. Despite richly characterizing the interdependent effects of the input components on the output of f with a factor graph, DEC-HBO can still guarantee no-regret performance asymptotically. Empirical evaluation on synthetic and real-world experiments (e.g., sparse Gaussian process model with 1811 hyperparameters) shows that DEC-HBO outperforms the state-of-the-art HBO algorithms.

A Generalized Stochastic Variational Bayesian Hyperparameter Learning Framework for Sparse Spectrum Gaussian Process Regression

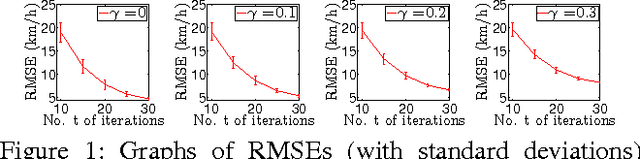
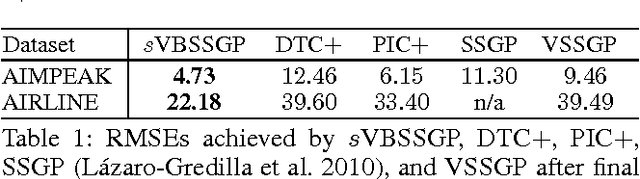
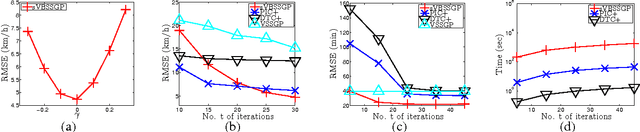
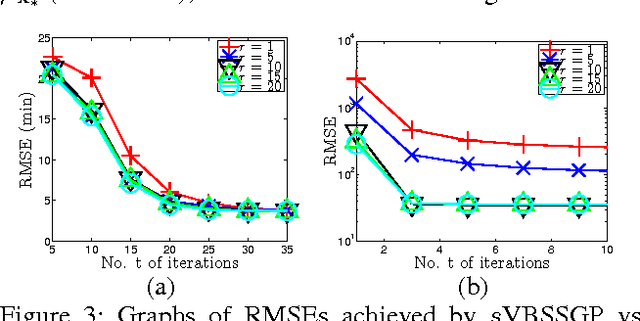
While much research effort has been dedicated to scaling up sparse Gaussian process (GP) models based on inducing variables for big data, little attention is afforded to the other less explored class of low-rank GP approximations that exploit the sparse spectral representation of a GP kernel. This paper presents such an effort to advance the state of the art of sparse spectrum GP models to achieve competitive predictive performance for massive datasets. Our generalized framework of stochastic variational Bayesian sparse spectrum GP (sVBSSGP) models addresses their shortcomings by adopting a Bayesian treatment of the spectral frequencies to avoid overfitting, modeling these frequencies jointly in its variational distribution to enable their interaction a posteriori, and exploiting local data for boosting the predictive performance. However, such structural improvements result in a variational lower bound that is intractable to be optimized. To resolve this, we exploit a variational parameterization trick to make it amenable to stochastic optimization. Interestingly, the resulting stochastic gradient has a linearly decomposable structure that can be exploited to refine our stochastic optimization method to incur constant time per iteration while preserving its property of being an unbiased estimator of the exact gradient of the variational lower bound. Empirical evaluation on real-world datasets shows that sVBSSGP outperforms state-of-the-art stochastic implementations of sparse GP models.