An Active Learning Framework for Efficient Robust Policy Search

Robust Policy Search is the problem of learning policies that do not degrade in performance when subject to unseen environment model parameters. It is particularly relevant for transferring policies learned in a simulation environment to the real world. Several existing approaches involve sampling large batches of trajectories which reflect the differences in various possible environments, and then selecting some subset of these to learn robust policies, such as the ones that result in the worst performance. We propose an active learning based framework, EffAcTS, to selectively choose model parameters for this purpose so as to collect only as much data as necessary to select such a subset. We apply this framework to an existing method, namely EPOpt, and experimentally validate the gains in sample efficiency and the performance of our approach on standard continuous control tasks. We also present a Multi-Task Learning perspective to the problem of Robust Policy Search, and draw connections from our proposed framework to existing work on Multi-Task Learning.

Rate of Change Analysis for Interestingness Measures

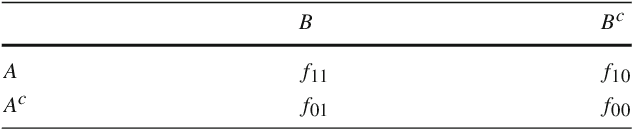
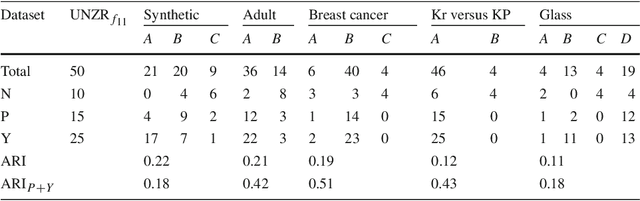
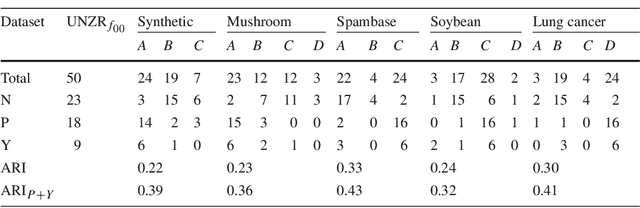
The use of Association Rule Mining techniques in diverse contexts and domains has resulted in the creation of numerous interestingness measures. This, in turn, has motivated researchers to come up with various classification schemes for these measures. One popular approach to classify the objective measures is to assess the set of mathematical properties they satisfy in order to help practitioners select the right measure for a given problem. In this research, we discuss the insufficiency of the existing properties in literature to capture certain behaviors of interestingness measures. This motivates us to present a novel approach to analyze and classify measures. We refer to this as a rate of change analysis (RCA). In this analysis a measure is described by how it varies if there is a unit change in the frequency count $(f_{11},f_{10},f_{01},f_{00})$, for different pre-existing states of the frequency counts. More formally, we look at the first partial derivative of the measure with respect to the various frequency count variables. We then use this analysis to define two new properties, Unit-Null Asymptotic Invariance (UNAI) and Unit-Null Zero Rate (UNZR). UNAI looks at the asymptotic effect of adding frequency patterns, while UNZR looks at the initial effect of adding frequency patterns when they do not pre-exist in the dataset. We present a comprehensive analysis of 50 interestingness measures and classify them in accordance with the two properties. We also present empirical studies, involving both synthetic and real-world datasets, which are used to cluster various measures according to the rule ranking patterns of the measures. The study concludes with the observation that classification of measures using the empirical clusters share significant similarities to the classification of measures done through the properties presented in this research.

Efficient-UCBV: An Almost Optimal Algorithm using Variance Estimates

We propose a novel variant of the UCB algorithm (referred to as Efficient-UCB-Variance (EUCBV)) for minimizing cumulative regret in the stochastic multi-armed bandit (MAB) setting. EUCBV incorporates the arm elimination strategy proposed in UCB-Improved \citep{auer2010ucb}, while taking into account the variance estimates to compute the arms' confidence bounds, similar to UCBV \citep{audibert2009exploration}. Through a theoretical analysis we establish that EUCBV incurs a \emph{gap-dependent} regret bound of {\scriptsize $O\left( \dfrac{K\sigma^2_{\max} \log (T\Delta^2 /K)}{\Delta}\right)$} after $T$ trials, where $\Delta$ is the minimal gap between optimal and sub-optimal arms; the above bound is an improvement over that of existing state-of-the-art UCB algorithms (such as UCB1, UCB-Improved, UCBV, MOSS). Further, EUCBV incurs a \emph{gap-independent} regret bound of {\scriptsize $O\left(\sqrt{KT}\right)$} which is an improvement over that of UCB1, UCBV and UCB-Improved, while being comparable with that of MOSS and OCUCB. Through an extensive numerical study we show that EUCBV significantly outperforms the popular UCB variants (like MOSS, OCUCB, etc.) as well as Thompson sampling and Bayes-UCB algorithms.

Thresholding Bandits with Augmented UCB

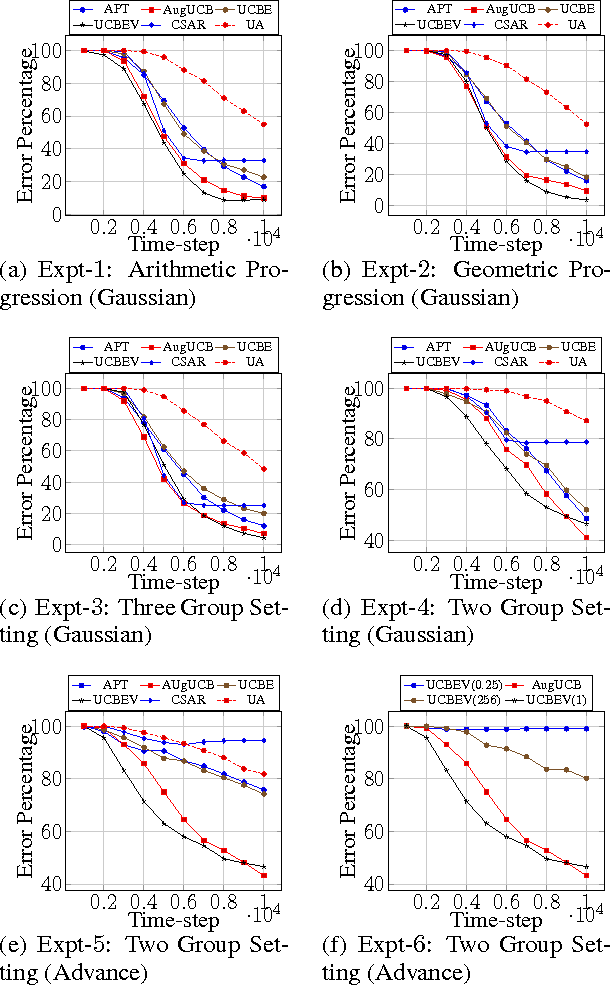
In this paper we propose the Augmented-UCB (AugUCB) algorithm for a fixed-budget version of the thresholding bandit problem (TBP), where the objective is to identify a set of arms whose quality is above a threshold. A key feature of AugUCB is that it uses both mean and variance estimates to eliminate arms that have been sufficiently explored; to the best of our knowledge this is the first algorithm to employ such an approach for the considered TBP. Theoretically, we obtain an upper bound on the loss (probability of mis-classification) incurred by AugUCB. Although UCBEV in literature provides a better guarantee, it is important to emphasize that UCBEV has access to problem complexity (whose computation requires arms' mean and variances), and hence is not realistic in practice; this is in contrast to AugUCB whose implementation does not require any such complexity inputs. We conduct extensive simulation experiments to validate the performance of AugUCB. Through our simulation work, we establish that AugUCB, owing to its utilization of variance estimates, performs significantly better than the state-of-the-art APT, CSAR and other non variance-based algorithms.

Linear Bandit algorithms using the Bootstrap

This study presents two new algorithms for solving linear stochastic bandit problems. The proposed methods use an approach from non-parametric statistics called bootstrapping to create confidence bounds. This is achieved without making any assumptions about the distribution of noise in the underlying system. We present the X-Random and X-Fixed bootstrap bandits which correspond to the two well-known approaches for conducting bootstraps on models, in the literature. The proposed methods are compared to other popular solutions for linear stochastic bandit problems, namely, OFUL, LinUCB and Thompson Sampling. The comparisons are carried out using a simulation study on a hierarchical probability meta-model, built from published data of experiments, which are run on real systems. The model representing the response surfaces is conceptualized as a Bayesian Network which is presented with varying degrees of noise for the simulations. One of the proposed methods, X-Random bootstrap, performs better than the baselines in-terms of cumulative regret across various degrees of noise and different number of trials. In certain settings the cumulative regret of this method is less than half of the best baseline. The X-Fixed bootstrap performs comparably in most situations and particularly well when the number of trials is low. The study concludes that these algorithms could be a preferred alternative for solving linear bandit problems, especially when the distribution of the noise in the system is unknown.