Muneeb Aadil
Causal Strategic Learning with Competitive Selection
Sep 05, 2023Abstract:We study the problem of agent selection in causal strategic learning under multiple decision makers and address two key challenges that come with it. Firstly, while much of prior work focuses on studying a fixed pool of agents that remains static regardless of their evaluations, we consider the impact of selection procedure by which agents are not only evaluated, but also selected. When each decision maker unilaterally selects agents by maximising their own utility, we show that the optimal selection rule is a trade-off between selecting the best agents and providing incentives to maximise the agents' improvement. Furthermore, this optimal selection rule relies on incorrect predictions of agents' outcomes. Hence, we study the conditions under which a decision maker's optimal selection rule will not lead to deterioration of agents' outcome nor cause unjust reduction in agents' selection chance. To that end, we provide an analytical form of the optimal selection rule and a mechanism to retrieve the causal parameters from observational data, under certain assumptions on agents' behaviour. Secondly, when there are multiple decision makers, the interference between selection rules introduces another source of biases in estimating the underlying causal parameters. To address this problem, we provide a cooperative protocol which all decision makers must collectively adopt to recover the true causal parameters. Lastly, we complement our theoretical results with simulation studies. Our results highlight not only the importance of causal modeling as a strategy to mitigate the effect of gaming, as suggested by previous work, but also the need of a benevolent regulator to enable it.
Preventing Clean Label Poisoning using Gaussian Mixture Loss
Feb 10, 2020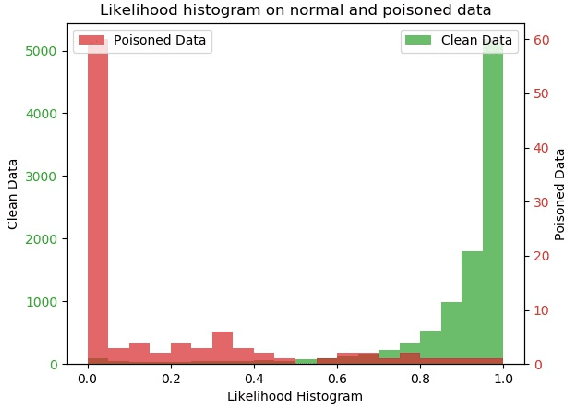
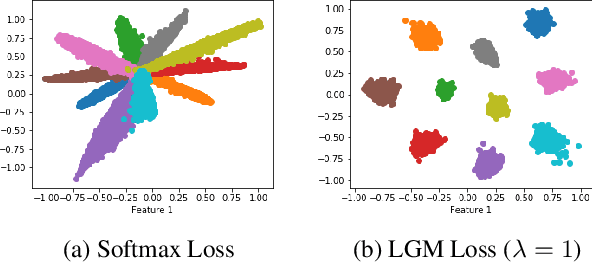
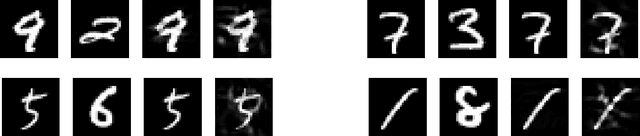
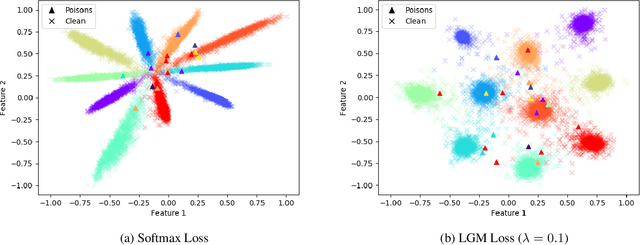
Abstract:Since 2014 when Szegedy et al. showed that carefully designed perturbations of the input can lead Deep Neural Networks (DNNs) to wrongly classify its label, there has been an ongoing research to make DNNs more robust to such malicious perturbations. In this work, we consider a poisoning attack called Clean Labeling poisoning attack (CLPA). The goal of CLPA is to inject seemingly benign instances which can drastically change decision boundary of the DNNs due to which subsequent queries at test time can be mis-classified. We argue that a strong defense against CLPA can be embedded into the model during the training by imposing features of the network to follow a Large Margin Gaussian Mixture distribution in the penultimate layer. By having such a prior knowledge, we can systematically evaluate how unusual the example is, given the label it is claiming to be. We demonstrate our builtin defense via experiments on MNIST and CIFAR datasets. We train two models on each dataset: one trained via softmax, another via LGM. We show that using LGM can substantially reduce the effectiveness of CLPA while having no additional overhead of data sanitization. The code to reproduce our results is available online.
Improving Super-Resolution Methods via Incremental Residual Learning
Aug 21, 2018


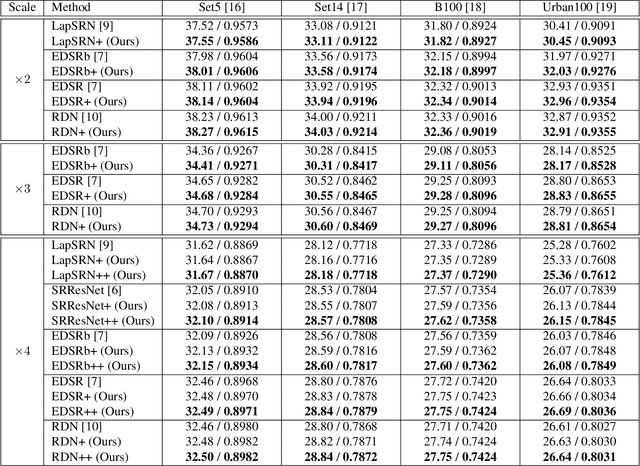
Abstract:Recently, deep Convolutional Neural Networks (CNNs) have shown promising performance in accurate reconstruction of high resolution (HR) image, given its low resolution (LR) counter-part. However, recent state-of-the-art methods operate primarily on LR image for memory efficiency, but we show that it comes at the cost of performance. Furthermore, because spatial dimensions of input and output of such networks do not match, it's not possible to learn residuals in image space; we show that learning residuals in image space leads to performance enhancement. To this end, we propose a novel Incremental Residual Learning (IRL) framework to solve the above mentioned issues. In IRL, a set of branches i.e arbitrary image-to-image networks are trained sequentially where each branch takes spatially upsampled higher dimensional feature maps as input and predicts the residuals of all previous branches combined. We plug recent state of the art methods as base networks in IRL framework and demonstrate the consistent performance enhancement through extensive experiments on public benchmark datasets to set a new state of the art for super-resolution. Compared to the base networks our method incurs no extra memory overhead as only one branch is trained at a time. Furthermore, as our method is trained to learned residuals, complete set of branches are trained in only 20% of time relative to base network.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge