Wasserstein Robust Reinforcement Learning

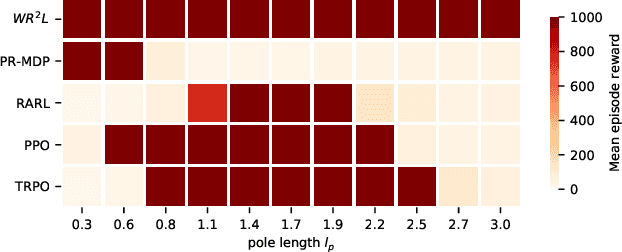
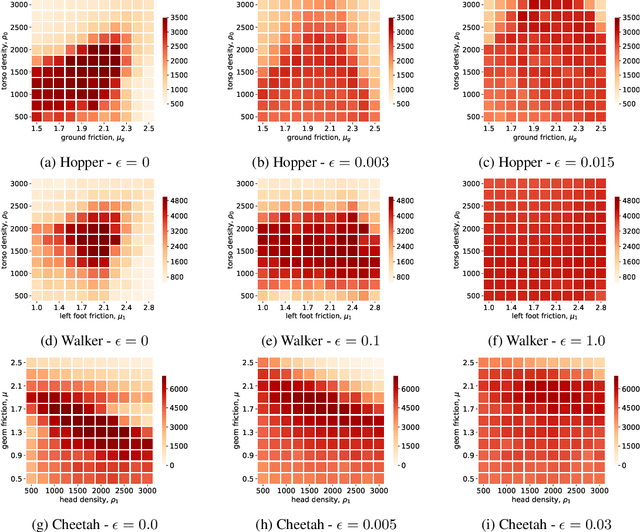
Reinforcement learning algorithms, though successful, tend to over-fit to training environments hampering their application to the real-world. This paper proposes $\text{W}\text{R}^{2}\text{L}$ -- a robust reinforcement learning algorithm with significant robust performance on low and high-dimensional control tasks. Our method formalises robust reinforcement learning as a novel min-max game with a Wasserstein constraint for a correct and convergent solver. Apart from the formulation, we also propose an efficient and scalable solver following a novel zero-order optimisation method that we believe can be useful to numerical optimisation in general. We empirically demonstrate significant gains compared to standard and robust state-of-the-art algorithms on high-dimensional MuJuCo environments.

A note on reinforcement learning with Wasserstein distance regularisation, with applications to multipolicy learning

In this note we describe an application of Wasserstein distance to Reinforcement Learning. The Wasserstein distance in question is between the distribution of mappings of trajectories of a policy into some metric space, and some other fixed distribution (which may, for example, come from another policy). Different policies induce different distributions, so given an underlying metric, the Wasserstein distance quantifies how different policies are. This can be used to learn multiple polices which are different in terms of such Wasserstein distances by using a Wasserstein regulariser. Changing the sign of the regularisation parameter, one can learn a policy for which its trajectory mapping distribution is attracted to a given fixed distribution.