Vladimir Milenkovic
Wasserstein Robust Reinforcement Learning
Sep 16, 2019
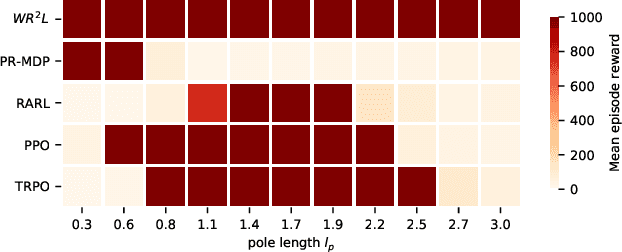

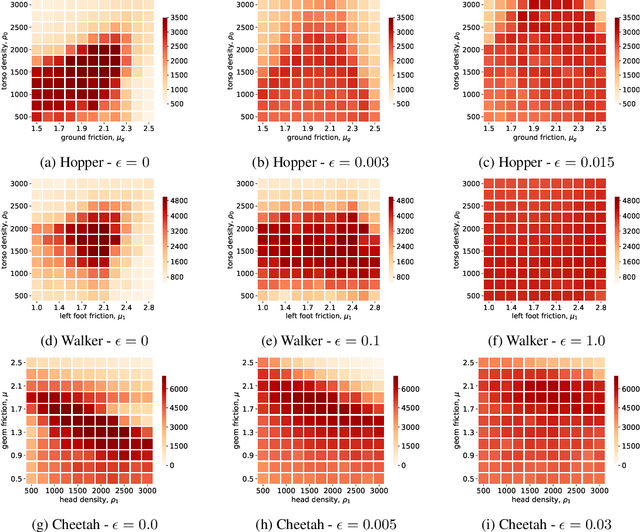
Abstract:Reinforcement learning algorithms, though successful, tend to over-fit to training environments hampering their application to the real-world. This paper proposes $\text{W}\text{R}^{2}\text{L}$ -- a robust reinforcement learning algorithm with significant robust performance on low and high-dimensional control tasks. Our method formalises robust reinforcement learning as a novel min-max game with a Wasserstein constraint for a correct and convergent solver. Apart from the formulation, we also propose an efficient and scalable solver following a novel zero-order optimisation method that we believe can be useful to numerical optimisation in general. We empirically demonstrate significant gains compared to standard and robust state-of-the-art algorithms on high-dimensional MuJuCo environments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge