MohammadJavad Azizi
Non-stationary Bandits and Meta-Learning with a Small Set of Optimal Arms
Mar 13, 2022



Abstract:We study a sequential decision problem where the learner faces a sequence of $K$-armed stochastic bandit tasks. The tasks may be designed by an adversary, but the adversary is constrained to choose the optimal arm of each task in a smaller (but unknown) subset of $M$ arms. The task boundaries might be known (the bandit meta-learning setting), or unknown (the non-stationary bandit setting), and the number of tasks $N$ as well as the total number of rounds $T$ are known ($N$ could be unknown in the meta-learning setting). We design an algorithm based on a reduction to bandit submodular maximization, and show that its regret in both settings is smaller than the simple baseline of $\tilde{O}(\sqrt{KNT})$ that can be obtained by using standard algorithms designed for non-stationary bandit problems. For the bandit meta-learning problem with fixed task length $\tau$, we show that the regret of the algorithm is bounded as $\tilde{O}(N\sqrt{M \tau}+N^{2/3})$. Under additional assumptions on the identifiability of the optimal arms in each task, we show a bandit meta-learning algorithm with an improved $\tilde{O}(N\sqrt{M \tau}+N^{1/2})$ regret.
Fixed-Budget Best-Arm Identification in Contextual Bandits: A Static-Adaptive Algorithm
Jun 22, 2021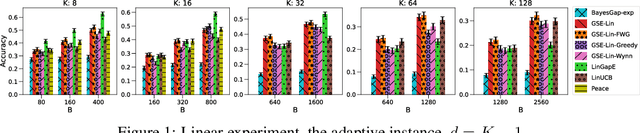
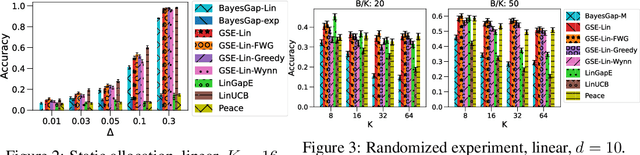
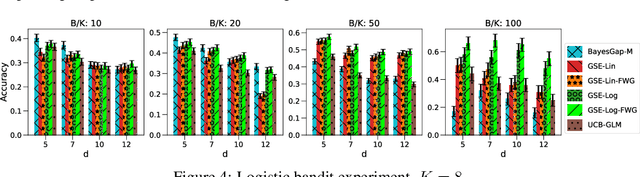
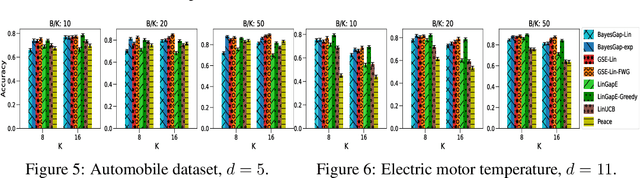
Abstract:We study the problem of best-arm identification (BAI) in contextual bandits in the fixed-budget setting. We propose a general successive elimination algorithm that proceeds in stages and eliminates a fixed fraction of suboptimal arms in each stage. This design takes advantage of the strengths of static and adaptive allocations. We analyze the algorithm in linear models and obtain a better error bound than prior work. We also apply it to generalized linear models (GLMs) and bound its error. This is the first BAI algorithm for GLMs in the fixed-budget setting. Our extensive numerical experiments show that our algorithm outperforms the state of art.
Guaranteed Fixed-Confidence Best Arm Identification in Multi-Armed Bandits: Simple Sequential Elimination Algorithms
Jun 22, 2021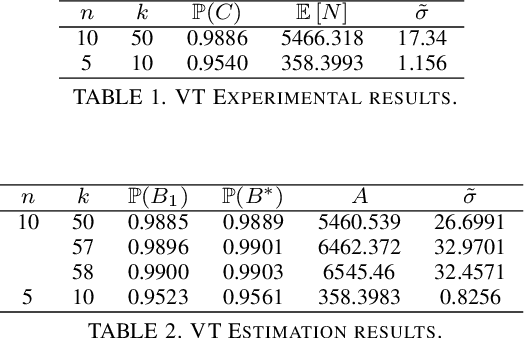
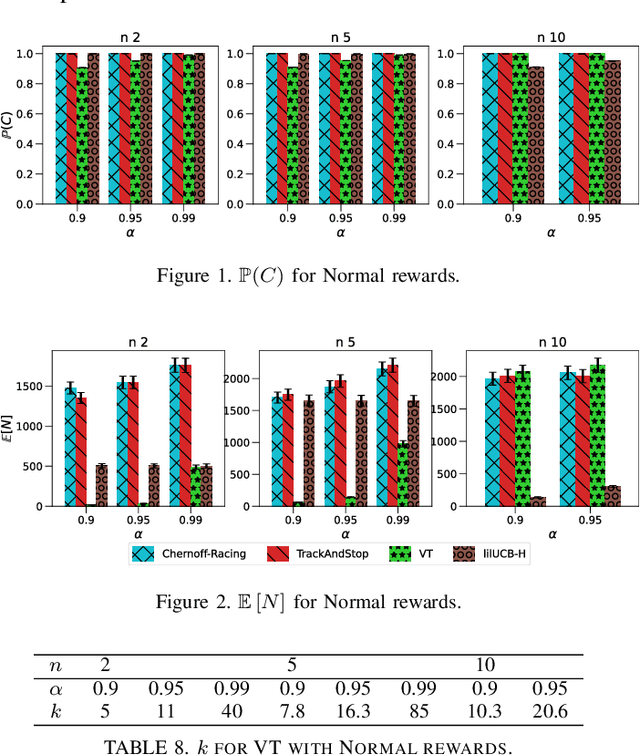
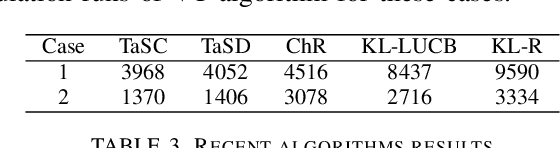
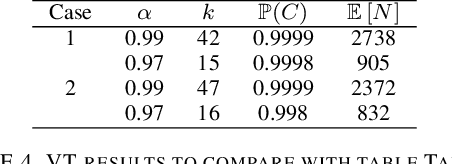
Abstract:We consider the problem of finding, through adaptive sampling, which of $n$ options (arms) has the largest mean. Our objective is to determine a rule which identifies the best arm with a fixed minimum confidence using as few observations as possible, i.e. this is a fixed-confidence (FC) best arm identification (BAI) in multi-armed bandits. We study such problems under the Bayesian setting with both Bernoulli and Gaussian arms. We propose to use the classical "vector at a time" (VT) rule, which samples each remaining arm once in each round. We show how VT can be implemented and analyzed in our Bayesian setting and be improved by early elimination. Our analysis show that these algorithms guarantee an optimal strategy under the prior. We also propose and analyze a variant of the classical "play the winner" (PW) algorithm. Numerical results show that these rules compare favorably with state-of-art algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge