Guaranteed Fixed-Confidence Best Arm Identification in Multi-Armed Bandits: Simple Sequential Elimination Algorithms
Paper and Code
Jun 22, 2021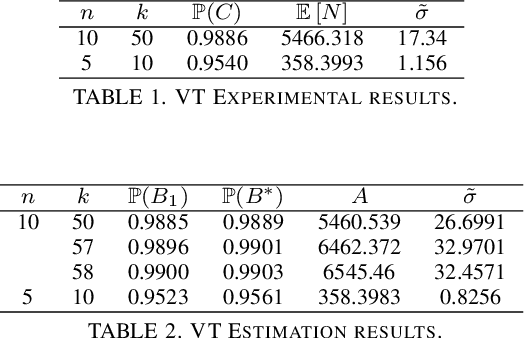
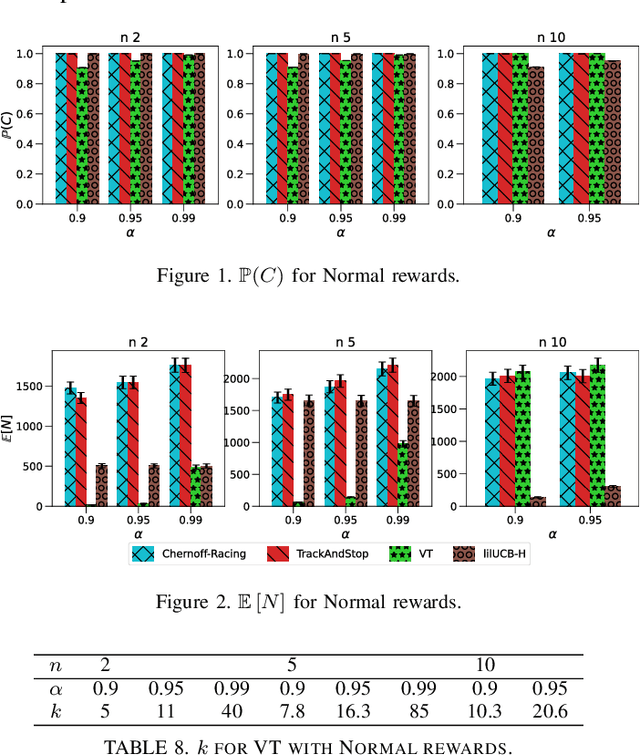
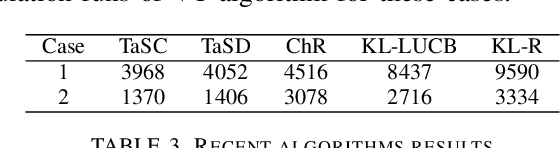
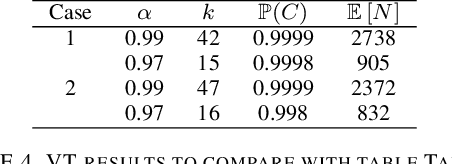
We consider the problem of finding, through adaptive sampling, which of $n$ options (arms) has the largest mean. Our objective is to determine a rule which identifies the best arm with a fixed minimum confidence using as few observations as possible, i.e. this is a fixed-confidence (FC) best arm identification (BAI) in multi-armed bandits. We study such problems under the Bayesian setting with both Bernoulli and Gaussian arms. We propose to use the classical "vector at a time" (VT) rule, which samples each remaining arm once in each round. We show how VT can be implemented and analyzed in our Bayesian setting and be improved by early elimination. Our analysis show that these algorithms guarantee an optimal strategy under the prior. We also propose and analyze a variant of the classical "play the winner" (PW) algorithm. Numerical results show that these rules compare favorably with state-of-art algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge