Mohammad Fereydounian
The Exact Class of Graph Functions Generated by Graph Neural Networks
Feb 17, 2022



Abstract:Given a graph function, defined on an arbitrary set of edge weights and node features, does there exist a Graph Neural Network (GNN) whose output is identical to the graph function? In this paper, we fully answer this question and characterize the class of graph problems that can be represented by GNNs. We identify an algebraic condition, in terms of the permutation of edge weights and node features, which proves to be necessary and sufficient for a graph problem to lie within the reach of GNNs. Moreover, we show that this condition can be efficiently verified by checking quadratically many constraints. Note that our refined characterization on the expressive power of GNNs are orthogonal to those theoretical results showing equivalence between GNNs and Weisfeiler-Lehman graph isomorphism heuristic. For instance, our characterization implies that many natural graph problems, such as min-cut value, max-flow value, and max-clique size, can be represented by a GNN. In contrast, and rather surprisingly, there exist very simple graphs for which no GNN can correctly find the length of the shortest paths between all nodes. Note that finding shortest paths is one of the most classical problems in Dynamic Programming (DP). Thus, the aforementioned negative example highlights the misalignment between DP and GNN, even though (conceptually) they follow very similar iterative procedures. Finally, we support our theoretical results by experimental simulations.
Safe Learning under Uncertain Objectives and Constraints
Jun 23, 2020
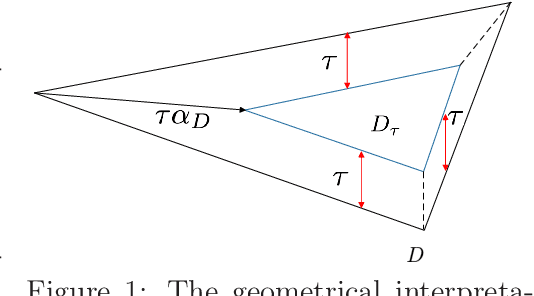
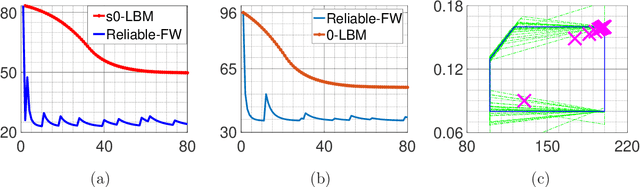
Abstract:In this paper, we consider non-convex optimization problems under \textit{unknown} yet safety-critical constraints. Such problems naturally arise in a variety of domains including robotics, manufacturing, and medical procedures, where it is infeasible to know or identify all the constraints. Therefore, the parameter space should be explored in a conservative way to ensure that none of the constraints are violated during the optimization process once we start from a safe initialization point. To this end, we develop an algorithm called Reliable Frank-Wolfe (Reliable-FW). Given a general non-convex function and an unknown polytope constraint, Reliable-FW simultaneously learns the landscape of the objective function and the boundary of the safety polytope. More precisely, by assuming that Reliable-FW has access to a (stochastic) gradient oracle of the objective function and a noisy feasibility oracle of the safety polytope, it finds an $\epsilon$-approximate first-order stationary point with the optimal ${\mathcal{O}}({1}/{\epsilon^2})$ gradient oracle complexity (resp. $\tilde{\mathcal{O}}({1}/{\epsilon^3})$ (also optimal) in the stochastic gradient setting), while ensuring the safety of all the iterates. Rather surprisingly, Reliable-FW only makes $\tilde{\mathcal{O}}(({d^2}/{\epsilon^2})\log 1/\delta)$ queries to the noisy feasibility oracle (resp. $\tilde{\mathcal{O}}(({d^2}/{\epsilon^4})\log 1/\delta)$ in the stochastic gradient setting) where $d$ is the dimension and $\delta$ is the reliability parameter, tightening the existing bounds even for safe minimization of convex functions. We further specialize our results to the case that the objective function is convex. A crucial component of our analysis is to introduce and apply a technique called geometric shrinkage in the context of safe optimization.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge