Safe Learning under Uncertain Objectives and Constraints
Paper and Code
Jun 23, 2020
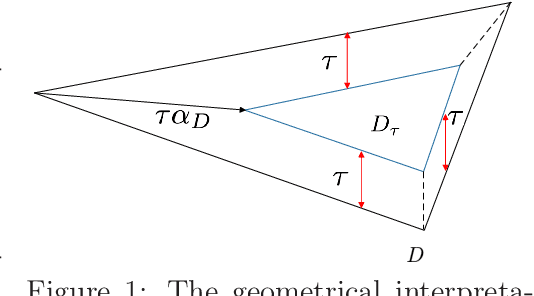
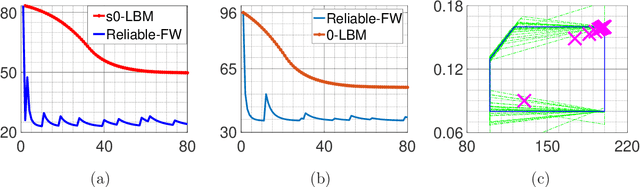
In this paper, we consider non-convex optimization problems under \textit{unknown} yet safety-critical constraints. Such problems naturally arise in a variety of domains including robotics, manufacturing, and medical procedures, where it is infeasible to know or identify all the constraints. Therefore, the parameter space should be explored in a conservative way to ensure that none of the constraints are violated during the optimization process once we start from a safe initialization point. To this end, we develop an algorithm called Reliable Frank-Wolfe (Reliable-FW). Given a general non-convex function and an unknown polytope constraint, Reliable-FW simultaneously learns the landscape of the objective function and the boundary of the safety polytope. More precisely, by assuming that Reliable-FW has access to a (stochastic) gradient oracle of the objective function and a noisy feasibility oracle of the safety polytope, it finds an $\epsilon$-approximate first-order stationary point with the optimal ${\mathcal{O}}({1}/{\epsilon^2})$ gradient oracle complexity (resp. $\tilde{\mathcal{O}}({1}/{\epsilon^3})$ (also optimal) in the stochastic gradient setting), while ensuring the safety of all the iterates. Rather surprisingly, Reliable-FW only makes $\tilde{\mathcal{O}}(({d^2}/{\epsilon^2})\log 1/\delta)$ queries to the noisy feasibility oracle (resp. $\tilde{\mathcal{O}}(({d^2}/{\epsilon^4})\log 1/\delta)$ in the stochastic gradient setting) where $d$ is the dimension and $\delta$ is the reliability parameter, tightening the existing bounds even for safe minimization of convex functions. We further specialize our results to the case that the objective function is convex. A crucial component of our analysis is to introduce and apply a technique called geometric shrinkage in the context of safe optimization.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge