Mithun Chakraborty
Policy Abstraction and Nash Refinement in Tree-Exploiting PSRO
Feb 05, 2025
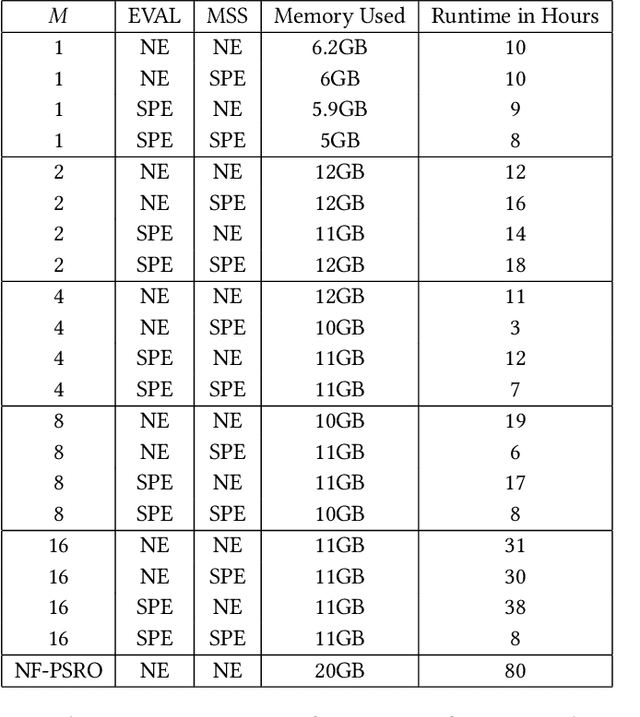

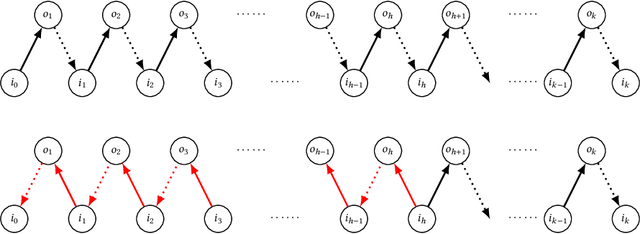
Abstract:Policy Space Response Oracles (PSRO) interleaves empirical game-theoretic analysis with deep reinforcement learning (DRL) to solve games too complex for traditional analytic methods. Tree-exploiting PSRO (TE-PSRO) is a variant of this approach that iteratively builds a coarsened empirical game model in extensive form using data obtained from querying a simulator that represents a detailed description of the game. We make two main methodological advances to TE-PSRO that enhance its applicability to complex games of imperfect information. First, we introduce a scalable representation for the empirical game tree where edges correspond to implicit policies learned through DRL. These policies cover conditions in the underlying game abstracted in the game model, supporting sustainable growth of the tree over epochs. Second, we leverage extensive form in the empirical model by employing refined Nash equilibria to direct strategy exploration. To enable this, we give a modular and scalable algorithm based on generalized backward induction for computing a subgame perfect equilibrium (SPE) in an imperfect-information game. We experimentally evaluate our approach on a suite of games including an alternating-offer bargaining game with outside offers; our results demonstrate that TE-PSRO converges toward equilibrium faster when new strategies are generated based on SPE rather than Nash equilibrium, and with reasonable time/memory requirements for the growing empirical model.
Finding Fair and Efficient Allocations When Valuations Don't Add Up
Mar 18, 2020



Abstract:In this paper, we present new results on the fair and efficient allocation of indivisible goods to agents that have monotone, submodular, non-additive valuation functions over bundles. Despite their simple structure, these agent valuations are a natural model for several real-world domains. We show that, if such a valuation function has binary marginal gains, a socially optimal (i.e. utilitarian social welfare-maximizing) allocation that achieves envy-freeness up to one item (EF1) exists and is computationally tractable. We also prove that the Nash welfare-maximizing and the leximin allocations both exhibit this fairness-efficiency combination, by showing that they can be achieved by minimizing any symmetric strictly convex function over utilitarian optimal outcomes. To the best of our knowledge, this is the first valuation function class not subsumed by additive valuations for which it has been established that an allocation maximizing Nash welfare is EF1. Moreover, for a subclass of these valuation functions based on maximum (unweighted) bipartite matching, we show that a leximin allocation can be computed in polynomial time.
On Weighted Envy-Freeness in Indivisible Item Allocation
Sep 24, 2019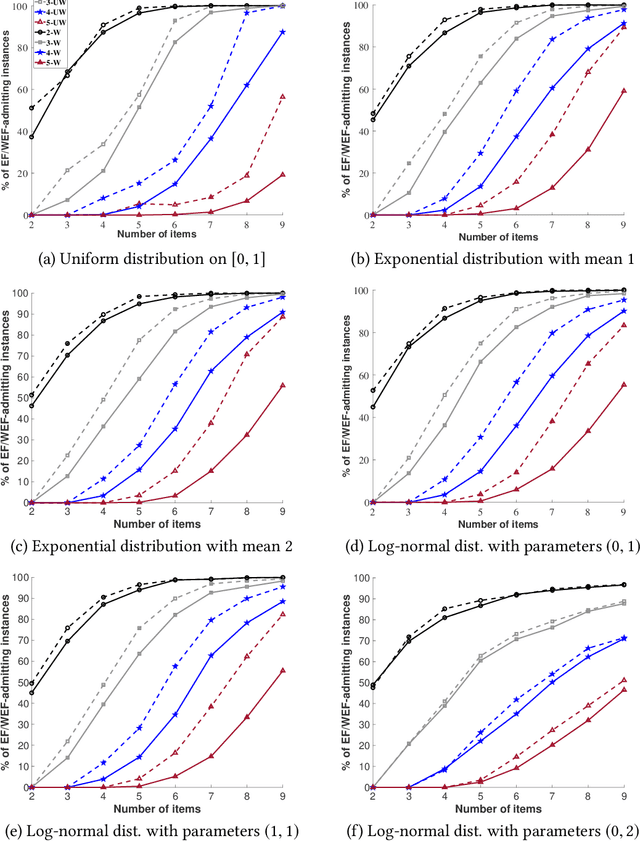
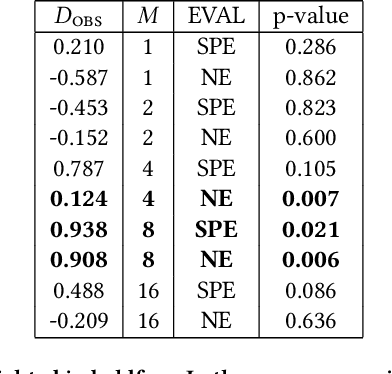
Abstract:In this paper, we introduce and analyze new envy-based fairness concepts for agents with weights: these weights regulate their mutual envy in a situation where indivisible goods are allocated to the agents. We propose two variants of envy-freeness up to one item for the weighted setting: in the strong variant, the envy can be eliminated by removing an item from the envied agent's bundle, whereas in the weak variant, envy can be eliminated by either removing an item from the envied agent's bundle or by replicating an item from the envied agent's bundle in the envying agent's bundle. We prove that for additive valuations, a strongly weighted envy-free allocation up to one item always exists and can be efficiently computed by means of a weight-based picking sequence. For two agents, we can also efficiently achieve strong weighted envy-freeness up to one item in conjunction with Pareto optimality using a weighted version of the classic adjusted winner algorithm. In addition, we show that an allocation that maximizes the weighted Nash social welfare always satisfies weak weighted envy-freeness up to one item, but may fail to satisfy the strong version of this property.
The Price of Diversity in Assignment Problems
Sep 12, 2018



Abstract:We introduce and analyze an extension to the matching problem on a weighted bipartite graph: Assignment with Type Constraints. The two parts of the graph are partitioned into subsets called types and blocks; we seek a matching with the largest sum of weights under the constraint that there is a pre-specified cap on the number of vertices matched in every type-block pair. Our primary motivation stems from the public housing program of Singapore, accounting for over 70% of its residential real estate. To promote ethnic diversity within its housing projects, Singapore imposes ethnicity quotas: each new housing development comprises blocks of flats and each ethnicity-based group in the population must not own more than a certain percentage of flats in a block. Other domains using similar hard capacity constraints include matching prospective students to schools or medical residents to hospitals. Limiting agents' choices for ensuring diversity in this manner naturally entails some welfare loss. One of our goals is to study the trade-off between diversity and social welfare in such settings. We first show that, while the classic assignment program is polynomial-time computable, adding diversity constraints makes it computationally intractable; however, we identify a $\tfrac{1}{2}$-approximation algorithm, as well as reasonable assumptions on the weights that permit poly-time algorithms. Next, we provide two upper bounds on the price of diversity -- a measure of the loss in welfare incurred by imposing diversity constraints -- as functions of natural problem parameters. We conclude the paper with simulations based on publicly available data from two diversity-constrained allocation problems -- Singapore Public Housing and Chicago School Choice -- which shed light on how the constrained maximization as well as lottery-based variants perform in practice.
How to show a probabilistic model is better
Feb 11, 2015Abstract:We present a simple theoretical framework, and corresponding practical procedures, for comparing probabilistic models on real data in a traditional machine learning setting. This framework is based on the theory of proper scoring rules, but requires only basic algebra and probability theory to understand and verify. The theoretical concepts presented are well-studied, primarily in the statistics literature. The goal of this paper is to advocate their wider adoption for performance evaluation in empirical machine learning.
Near-Optimal Target Learning With Stochastic Binary Signals
Feb 14, 2012
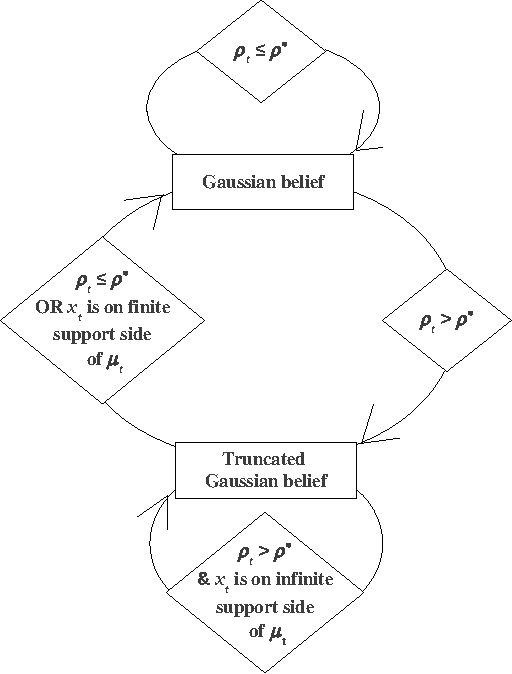


Abstract:We study learning in a noisy bisection model: specifically, Bayesian algorithms to learn a target value V given access only to noisy realizations of whether V is less than or greater than a threshold theta. At step t = 0, 1, 2, ..., the learner sets threshold theta t and observes a noisy realization of sign(V - theta t). After T steps, the goal is to output an estimate V^ which is within an eta-tolerance of V . This problem has been studied, predominantly in environments with a fixed error probability q < 1/2 for the noisy realization of sign(V - theta t). In practice, it is often the case that q can approach 1/2, especially as theta -> V, and there is little known when this happens. We give a pseudo-Bayesian algorithm which provably converges to V. When the true prior matches our algorithm's Gaussian prior, we show near-optimal expected performance. Our methods extend to the general multiple-threshold setting where the observation noisily indicates which of k >= 2 regions V belongs to.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge