On Weighted Envy-Freeness in Indivisible Item Allocation

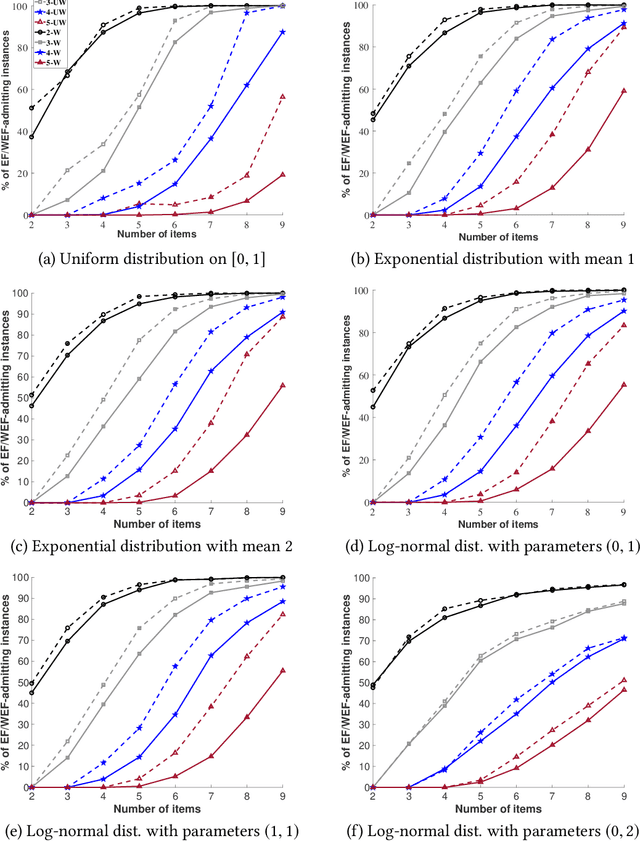
In this paper, we introduce and analyze new envy-based fairness concepts for agents with weights: these weights regulate their mutual envy in a situation where indivisible goods are allocated to the agents. We propose two variants of envy-freeness up to one item for the weighted setting: in the strong variant, the envy can be eliminated by removing an item from the envied agent's bundle, whereas in the weak variant, envy can be eliminated by either removing an item from the envied agent's bundle or by replicating an item from the envied agent's bundle in the envying agent's bundle. We prove that for additive valuations, a strongly weighted envy-free allocation up to one item always exists and can be efficiently computed by means of a weight-based picking sequence. For two agents, we can also efficiently achieve strong weighted envy-freeness up to one item in conjunction with Pareto optimality using a weighted version of the classic adjusted winner algorithm. In addition, we show that an allocation that maximizes the weighted Nash social welfare always satisfies weak weighted envy-freeness up to one item, but may fail to satisfy the strong version of this property.