Near-Optimal Target Learning With Stochastic Binary Signals
Paper and Code
Feb 14, 2012
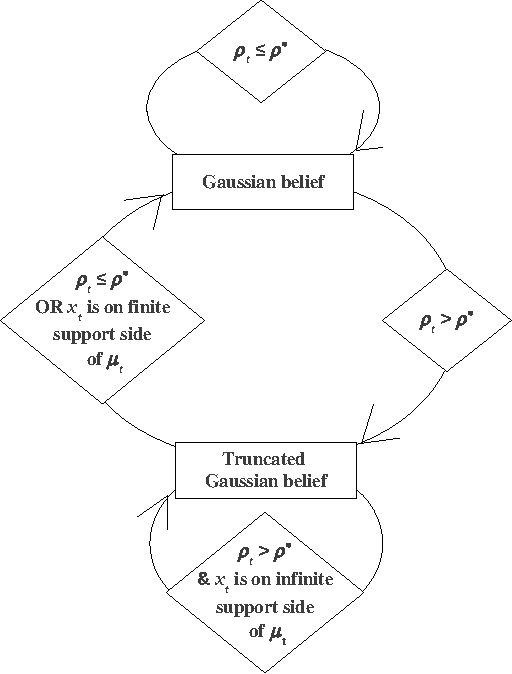


We study learning in a noisy bisection model: specifically, Bayesian algorithms to learn a target value V given access only to noisy realizations of whether V is less than or greater than a threshold theta. At step t = 0, 1, 2, ..., the learner sets threshold theta t and observes a noisy realization of sign(V - theta t). After T steps, the goal is to output an estimate V^ which is within an eta-tolerance of V . This problem has been studied, predominantly in environments with a fixed error probability q < 1/2 for the noisy realization of sign(V - theta t). In practice, it is often the case that q can approach 1/2, especially as theta -> V, and there is little known when this happens. We give a pseudo-Bayesian algorithm which provably converges to V. When the true prior matches our algorithm's Gaussian prior, we show near-optimal expected performance. Our methods extend to the general multiple-threshold setting where the observation noisily indicates which of k >= 2 regions V belongs to.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge