Collapsible Linear Blocks for Super-Efficient Super Resolution

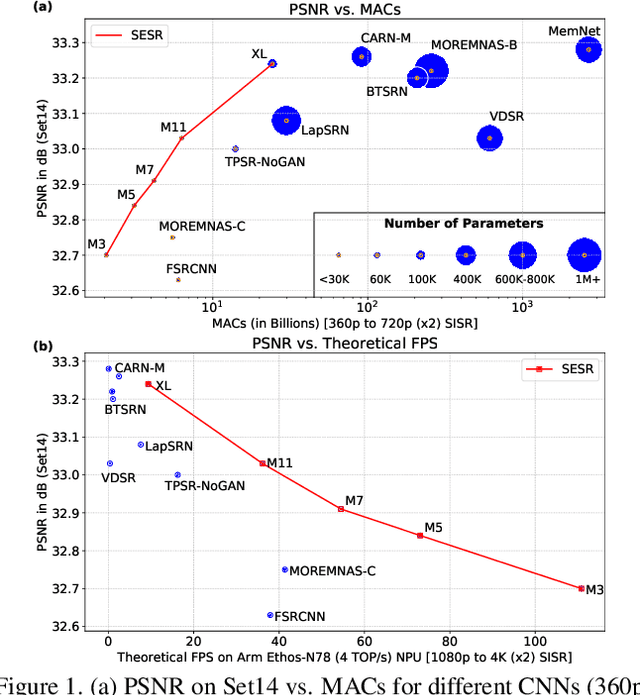
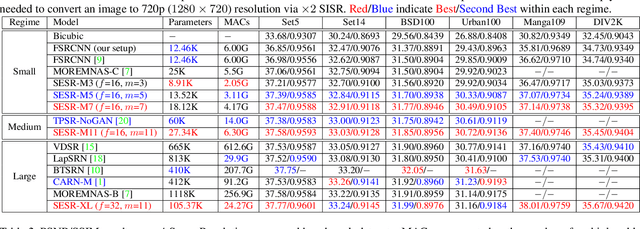
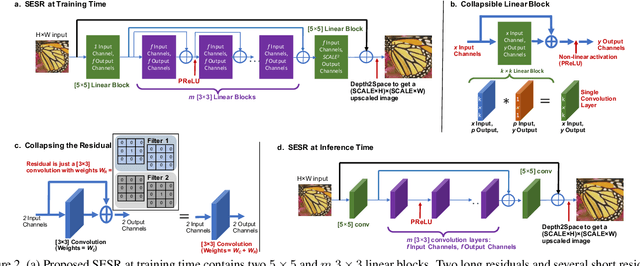
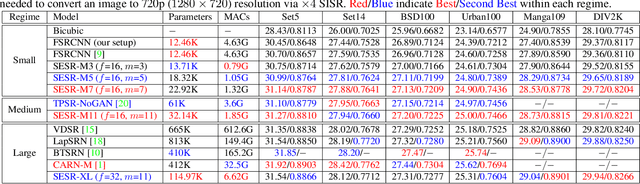
With the advent of smart devices that support 4K and 8K resolution, Single Image Super Resolution (SISR) has become an important computer vision problem. However, most super resolution deep networks are computationally very expensive. In this paper, we propose SESR, a new class of Super-Efficient Super Resolution networks that significantly improve image quality and reduce computational complexity. Detailed experiments across six benchmark datasets demonstrate that SESR achieves similar or better image quality than state-of-the-art models while requiring 2x to 330x fewer Multiply-Accumulate (MAC) operations. As a result, SESR can be used on constrained hardware to perform x2 (1080p to 4K) and x4 SISR (1080p to 8K). Towards this, we simulate hardware performance numbers for a commercial mobile Neural Processing Unit (NPU) for 1080p to 4K (x2) and 1080p to 8K (x4) SISR. Our results highlight the challenges faced by super resolution on AI accelerators and demonstrate that SESR is significantly faster than existing models. Overall, SESR establishes a new Pareto frontier on the quality (PSNR)-computation relationship for the super resolution task.

Solving Irregular and Data-enriched Differential Equations using Deep Neural Networks

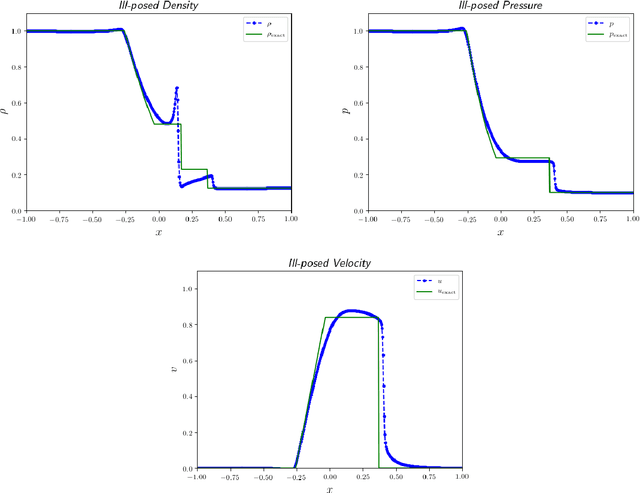
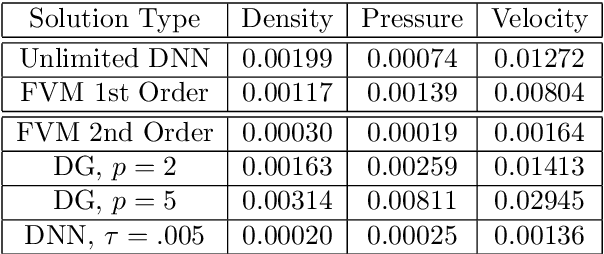
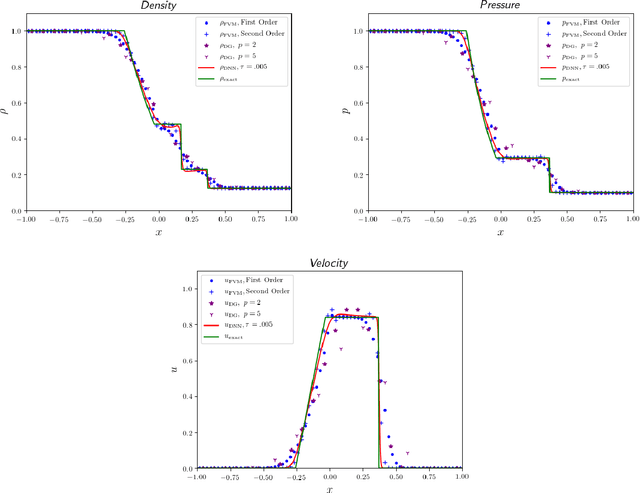
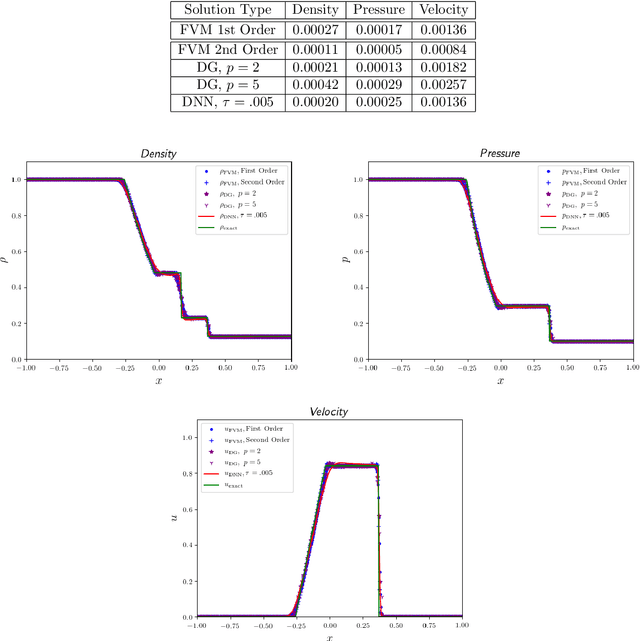
Recent work has introduced a simple numerical method for solving partial differential equations (PDEs) with deep neural networks (DNNs). This paper reviews and extends the method while applying it to analyze one of the most fundamental features in numerical PDEs and nonlinear analysis: irregular solutions. First, the Sod shock tube solution to compressible Euler equations is discussed, analyzed, and then compared to conventional finite element and finite volume methods. These methods are extended to consider performance improvements and simultaneous parameter space exploration. Next, a shock solution to compressible magnetohydrodynamics (MHD) is solved for, and used in a scenario where experimental data is utilized to enhance a PDE system that is \emph{a priori} insufficient to validate against the observed/experimental data. This is accomplished by enriching the model PDE system with source terms and using supervised training on synthetic experimental data. The resulting DNN framework for PDEs seems to demonstrate almost fantastical ease of system prototyping, natural integration of large data sets (be they synthetic or experimental), all while simultaneously enabling single-pass exploration of the entire parameter space.