KAM -- a Kernel Attention Module for Emotion Classification with EEG Data

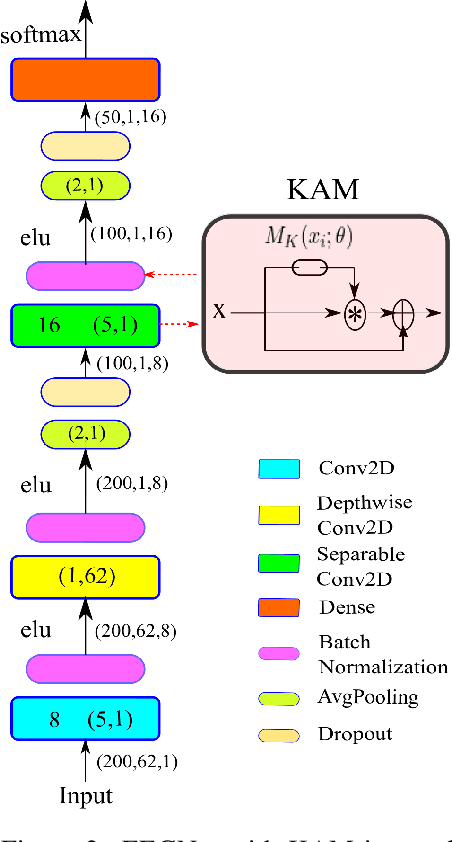
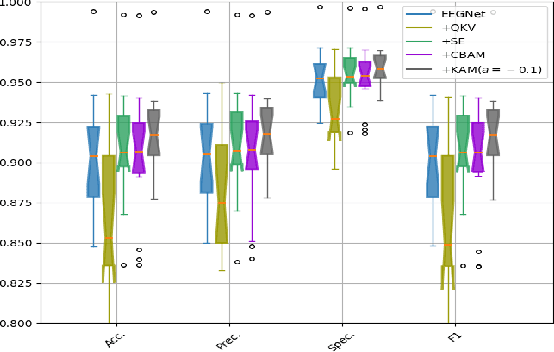
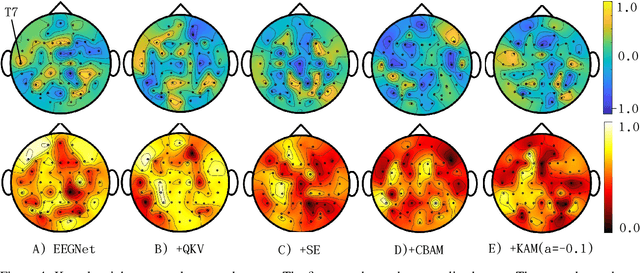
In this work, a kernel attention module is presented for the task of EEG-based emotion classification with neural networks. The proposed module utilizes a self-attention mechanism by performing a kernel trick, demanding significantly fewer trainable parameters and computations than standard attention modules. The design also provides a scalar for quantitatively examining the amount of attention assigned during deep feature refinement, hence help better interpret a trained model. Using EEGNet as the backbone model, extensive experiments are conducted on the SEED dataset to assess the module's performance on within-subject classification tasks compared to other SOTA attention modules. Requiring only one extra parameter, the inserted module is shown to boost the base model's mean prediction accuracy up to more than 1\% across 15 subjects. A key component of the method is the interpretability of solutions, which is addressed using several different techniques, and is included throughout as part of the dependency analysis.

A Monotonicity Constrained Attention Module for Emotion Classification with Limited EEG Data

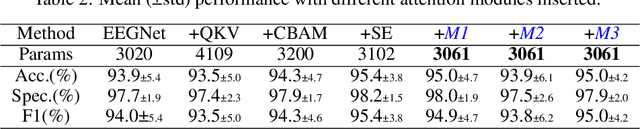
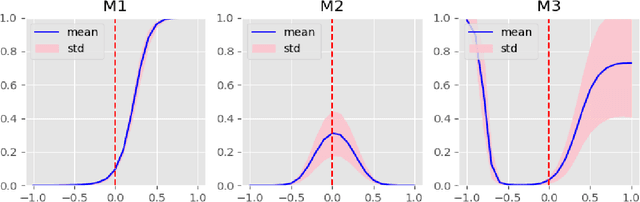
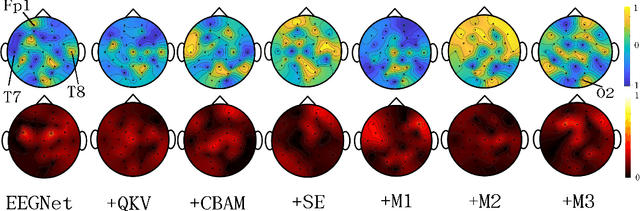
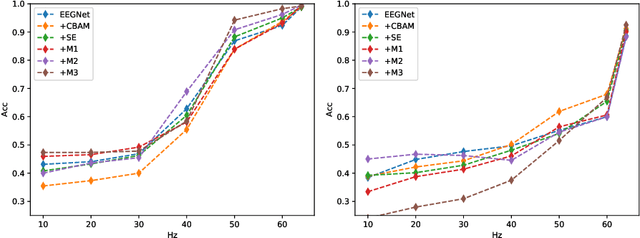
In this work, a parameter-efficient attention module is presented for emotion classification using a limited, or relatively small, number of electroencephalogram (EEG) signals. This module is called the Monotonicity Constrained Attention Module (MCAM) due to its capability of incorporating priors on the monotonicity when converting features' Gram matrices into attention matrices for better feature refinement. Our experiments have shown that MCAM's effectiveness is comparable to state-of-the-art attention modules in boosting the backbone network's performance in prediction while requiring less parameters. Several accompanying sensitivity analyses on trained models' prediction concerning different attacks are also performed. These attacks include various frequency domain filtering levels and gradually morphing between samples associated with multiple labels. Our results can help better understand different modules' behaviour in prediction and can provide guidance in applications where data is limited and are with noises.

Solving Irregular and Data-enriched Differential Equations using Deep Neural Networks

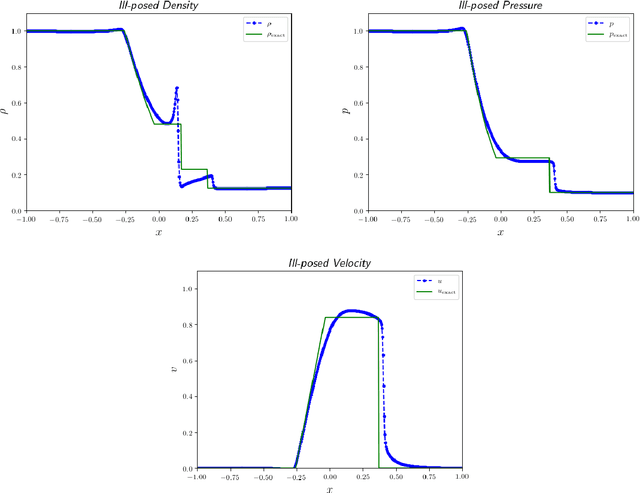
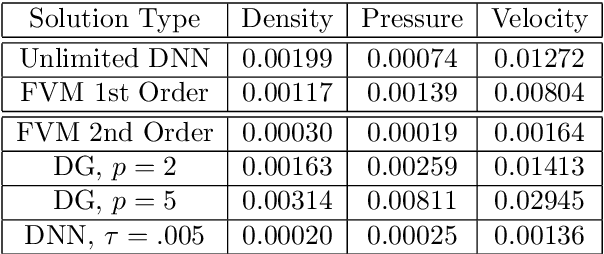
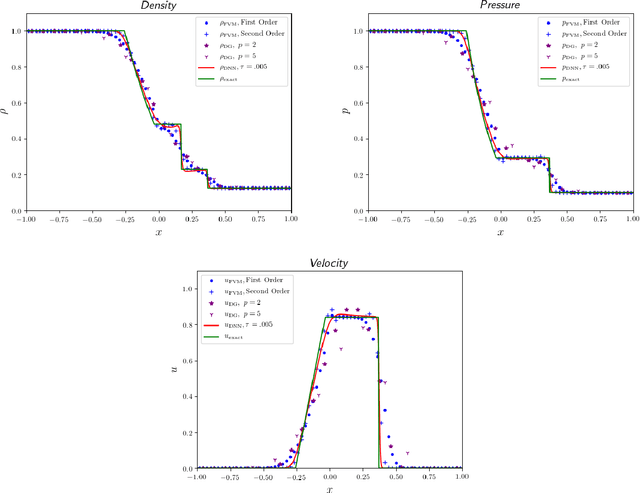
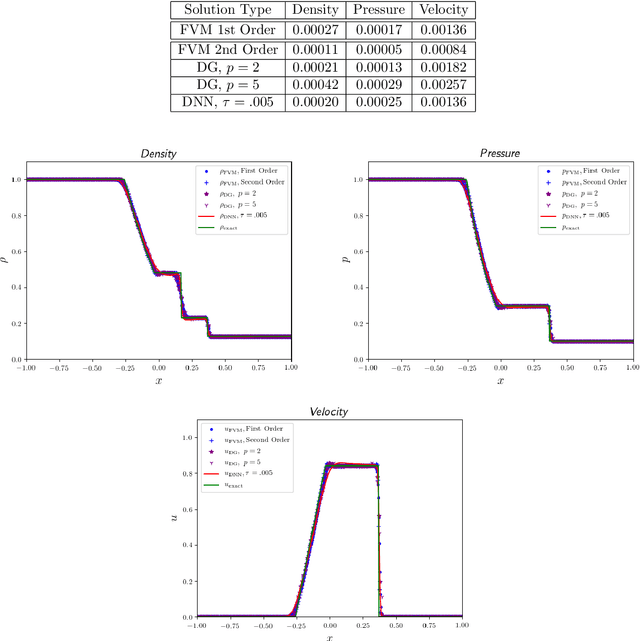
Recent work has introduced a simple numerical method for solving partial differential equations (PDEs) with deep neural networks (DNNs). This paper reviews and extends the method while applying it to analyze one of the most fundamental features in numerical PDEs and nonlinear analysis: irregular solutions. First, the Sod shock tube solution to compressible Euler equations is discussed, analyzed, and then compared to conventional finite element and finite volume methods. These methods are extended to consider performance improvements and simultaneous parameter space exploration. Next, a shock solution to compressible magnetohydrodynamics (MHD) is solved for, and used in a scenario where experimental data is utilized to enhance a PDE system that is \emph{a priori} insufficient to validate against the observed/experimental data. This is accomplished by enriching the model PDE system with source terms and using supervised training on synthetic experimental data. The resulting DNN framework for PDEs seems to demonstrate almost fantastical ease of system prototyping, natural integration of large data sets (be they synthetic or experimental), all while simultaneously enabling single-pass exploration of the entire parameter space.