Evaluating Model Performance Under Worst-case Subpopulations

The performance of ML models degrades when the training population is different from that seen under operation. Towards assessing distributional robustness, we study the worst-case performance of a model over all subpopulations of a given size, defined with respect to core attributes Z. This notion of robustness can consider arbitrary (continuous) attributes Z, and automatically accounts for complex intersectionality in disadvantaged groups. We develop a scalable yet principled two-stage estimation procedure that can evaluate the robustness of state-of-the-art models. We prove that our procedure enjoys several finite-sample convergence guarantees, including dimension-free convergence. Instead of overly conservative notions based on Rademacher complexities, our evaluation error depends on the dimension of Z only through the out-of-sample error in estimating the performance conditional on Z. On real datasets, we demonstrate that our method certifies the robustness of a model and prevents deployment of unreliable models.

Should Bank Stress Tests Be Fair?

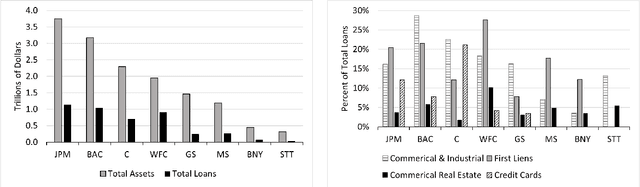
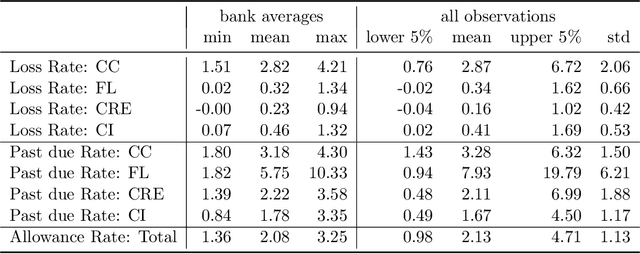
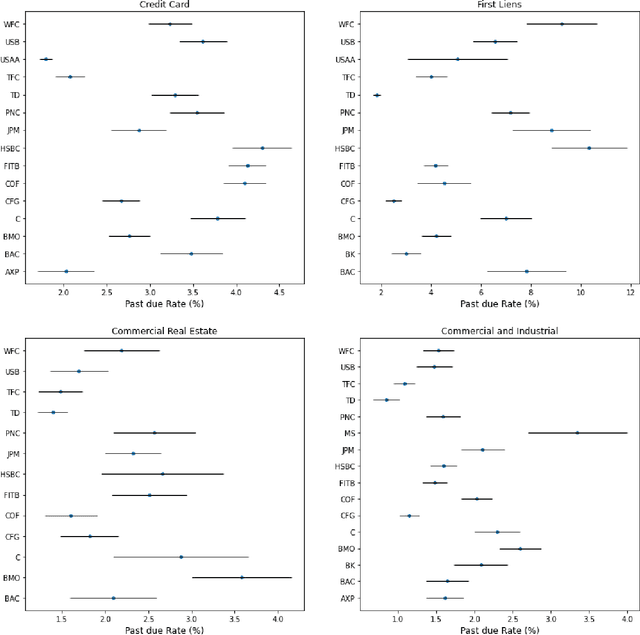
Regulatory stress tests have become the primary tool for setting capital requirements at the largest U.S. banks. The Federal Reserve uses confidential models to evaluate bank-specific outcomes for bank-specific portfolios in shared stress scenarios. As a matter of policy, the same models are used for all banks, despite considerable heterogeneity across institutions; individual banks have contended that some models are not suited to their businesses. Motivated by this debate, we ask, what is a fair aggregation of individually tailored models into a common model? We argue that simply pooling data across banks treats banks equally but is subject to two deficiencies: it may distort the impact of legitimate portfolio features, and it is vulnerable to implicit misdirection of legitimate information to infer bank identity. We compare various notions of regression fairness to address these deficiencies, considering both forecast accuracy and equal treatment. In the setting of linear models, we argue for estimating and then discarding centered bank fixed effects as preferable to simply ignoring differences across banks. We present evidence that the overall impact can be material. We also discuss extensions to nonlinear models.

Robust fine-tuning of zero-shot models

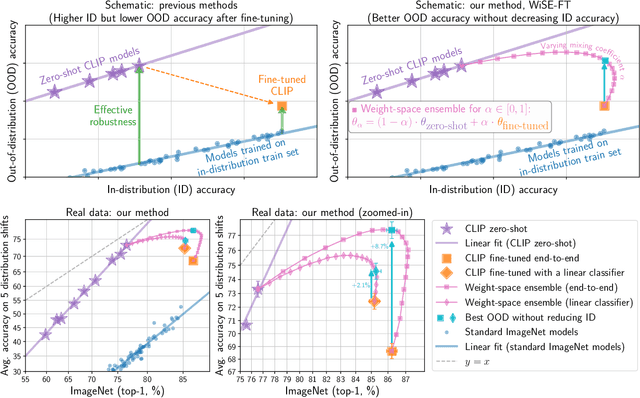
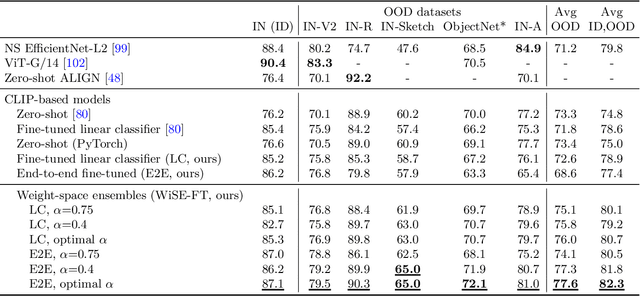
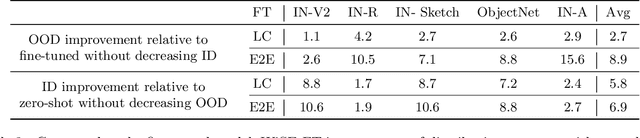
Large pre-trained models such as CLIP offer consistent accuracy across a range of data distributions when performing zero-shot inference (i.e., without fine-tuning on a specific dataset). Although existing fine-tuning approaches substantially improve accuracy in-distribution, they also reduce out-of-distribution robustness. We address this tension by introducing a simple and effective method for improving robustness: ensembling the weights of the zero-shot and fine-tuned models. Compared to standard fine-tuning, the resulting weight-space ensembles provide large accuracy improvements out-of-distribution, while matching or improving in-distribution accuracy. On ImageNet and five derived distribution shifts, weight-space ensembles improve out-of-distribution accuracy by 2 to 10 percentage points while increasing in-distribution accuracy by nearly 1 percentage point relative to standard fine-tuning. These improvements come at no additional computational cost during fine-tuning or inference.

Linear Classifiers Under Infinite Imbalance

We study the behavior of linear discriminant functions for binary classification in the infinite-imbalance limit, where the sample size of one class grows without bound while the sample size of the other remains fixed. The coefficients of the classifier minimize an expected loss specified through a weight function. We show that for a broad class of weight functions, the intercept diverges but the rest of the coefficient vector has a finite limit under infinite imbalance, extending prior work on logistic regression. The limit depends on the left tail of the weight function, for which we distinguish three cases: bounded, asymptotically polynomial, and asymptotically exponential. The limiting coefficient vectors reflect robustness or conservatism properties in the sense that they optimize against certain worst-case alternatives. In the bounded and polynomial cases, the limit is equivalent to an implicit choice of upsampling distribution for the minority class. We apply these ideas in a credit risk setting, with particular emphasis on performance in the high-sensitivity and high-specificity regions.

Peak Alignment of GC-MS Data with Deep Learning

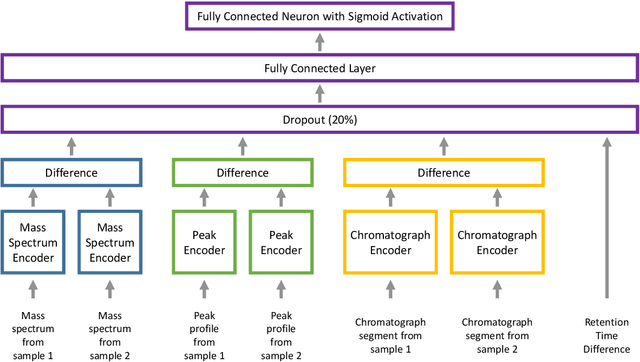
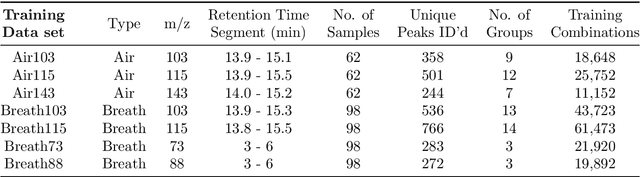
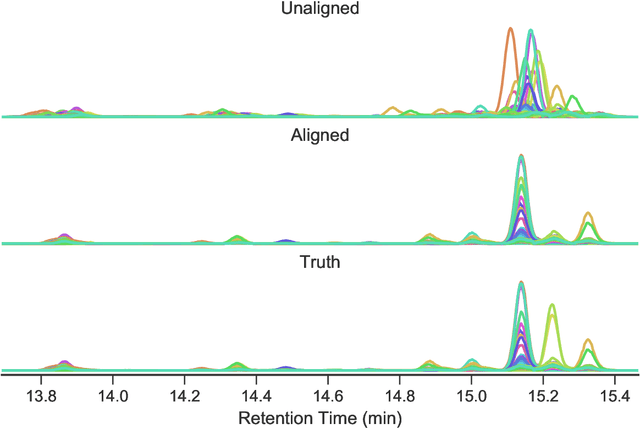
We present ChromAlignNet, a deep learning model for alignment of peaks in Gas Chromatogram-Mass Spectrometry (GC-MS) data. GC-MS is regarded as a gold standard in analysis of chemical composition in samples. However, due to the complexity of the instrument, a substance's retention time (RT) may not stay fixed across multiple GC-MS chromatograms. To use GC-MS data for biomarker discovery requires alignment of identical analyte's RT from different samples. Current methods of alignment are all based on a set of formal, mathematical rules, consequently, they are unable to handle the complexity of GC-MS data from human breath. We present a solution to GC-MS alignment using deep learning neural networks, which are more adept at complex, fuzzy data sets. We tested our model on several GC-MS data sets of various complexities and show the model has very good true position rates (up to 99% for easy data sets and up to 92% for very complex data sets). We compared our model with the popular correlation optimized warping (COW) and show our model has much better overall performance. This method can easily be adapted to other similar data such as those from liquid chromatography.